vsoch

Plot.ly, for instant sharing of graphs from R, Python, Matlab...

I have been unbelievably excited to test out plot.ly, specifically the API that is available for R, Python, Matlab, Julia, Arduino, Perl, and even REST.  As a graduate student that makes many plots, and then saves them as image files for upload somewhere, this instant-online-posting directly from my analysis software is sheer awesomeness.   I’ll walk through the relatively simple steps for one application, R:

Get Comfortable with plot.ly Interface

• First you need to sign up for a free account at plot.ly
• Find your API key.  When you log in, click on “Access Plotly” from the drop-down menu in the upper right

• Again, click on “Settings” from the drop-down in the upper right.  You will find your API key here!

• When you are logged in at https://plot.ly/plot, all of your uploaded charts can be seen by clicking the tiny folder in the upper left

Sending plots from R to plot.ly

Plot.ly has it’s own library, but I found that with my version of R, it told me that the plot.ly version wasn’t supported.  I found it best to install directly from github using devtools.  You can also source the main plotly script directly from github, however if you do this you will need to make sure that you have packages “RJSONIO” and “RCurl” installed.  To quickly post a plot from R to plot.ly, I made a little script that I can source, and then use with my data, username, and API key to create the plot:

code

You can then either go directly to the URL to see your plot, or log into plot.ly and click the folder icon in the top left.  This is just one example of using a boxplot - see https://plot.ly/api/ for many other examples and languages.  Feel free to tweak my boxplot script as a starting point for creating your own plots, because much of the code is by way of examples from their documentation.  Here is the finished plot (embedded in this post):

**As a disclaimer, keep in mind that the rules regarding data sharing and posting at your company or institution still apply!  While you can make a plot private, the data that you send to plotly would still be somewhere on their server, which would not be ok.  So - keep this in mind!

Export Data from R to Weka

This will be a quick post - I wanted to share an updated script to export a data frame from R to Weka.  The older version was poorly designed to take in two different data matrices (one for numerical, the other for demographic), and I realized how silly this was in retrospect.  The user would want to hand the function one data frame with everything!  The old link from my previous post will work, however I wanted to clarify a few things:

• Data is a matrix of size n by m, with m features defining n data objects.
• Row names and column names are used for data and feature labels, respectively.
• All variables are assumed to be numeric, with the exception of the row names (the “uid” variable), which is a string.
• Missing values, currently set as -9999 and NA, are recoded as “?” Change this section (line 28) to fit your data.
• If you have a nominal outcome variable (eg, you want to color your data by a label in Weka) change the variable type as follows:

@attribute groupVar {1,2}

with {1,2} corresponding to the set of options for the variable (these can also be strings).  You then want to select this variable in the dropdown next to “visualize all”

• More information on the .arff import format is available here.
• Edit the script to your liking, it’s pretty simple :O)

code

I am liking R a lot more than Matlab these days, oh dear!

Introduction to Weka

I’m new to using Weka, so I thought that it would be useful to log my steps.

Data Import

It’s likely that you will need to export your from your statistical software of choice by formatting it in the .arff file standard.  I wrote a script that exports from R, and could be easily tweaked.  When you start Weka, click on “Explorer” and “Open File” to import the .arff file.  If there is something wrong with your formatting, it will tell you.  Keep in mind that your data types (string, numeric, or nominal) will determine which kinds of analyses that you can do.  Missing values should be exported as question marks, ?.  When you import your data, Weka assumes that the last variable is your label of interest, so in my case this was a nominal variable with two classes, in the file, specified as:

@attribute RXStr {0,1}

You can also change this selection using the drop down menu above the graph visualization.  If you have a nominal variable selected, all of your features will be colored by these groups (eg, red and blue in the picture below).  Obviously, the list on the left are the attributes that you’ve loaded, and you can select each one by clicking on it, or using any of the buttons on top of the box.  Details for each feature are displayed on the right side of the GUI.

If you click on “edit” in the top right, you can see all of your data, and even click a box to edit it.

Data Preprocessing

It’s probably best to do normalization and other preprocessing before export, at least I don’t like some black box GUI getting all handsy with my data!  However, if you haven’t, you can click on “filters” above your features to see lots of options.  You can normalize, discretize, change variable types, the whole shabang!  I’m not a fan of this, but you can also replaceMissingValues, if your algorithm of choice doesn’t allow for them.  Feature selection is something else you might want to do, and while you have most power via the command line, you can use the GUI under “Select attributes” tab.  You can also choose a classifier of type “meta” that folds it into the algorithm.  I’m sure that there is a more elegant way of doing this, but after “selecting attributes” I right clicked on the result and saved my reduced set as a new data file to run analyses.

Classify (or Cluster)

The classify tab is where the meat of Weka is.  Remember that classify = “we have a label that we want to predict (supervised)” and cluster means “unsupervised.”  However, also note that Weka lets you validate an unsupervised clustering based on one of your variables.  On the top under “Choose” you can select your algorithm of choice, and the variable shown in the drop down menu is what you want to predict (normally it starts as your last variable imported).  An important note - the variable type that you have, and whether or not there are missing values, will determine which analyses you can do.  When your data doesn’t fit an algorithm, it will be greyed out.  Note that the filtering is done based on ALL of the variables that are in your feature list, regardless of whether they are checked or not.  For example, I had a string uid that was preventing me from being able to run most of the algorithms, and only when I clicked “remove” did they become available for selection. Once you’ve made it beyond these fussy data import details, the rest is pretty intuitive - you select an analysis, whether you want cross validation or to use a training set, and then click “Start.”

Visualize

The last useful tidbit is how to save and view your results.  If you right click on the analysis that you’ve just run in the list to the left, you can “save result buffer” and visualize (different visualizations depending on the algorithm).  You can also save the entire model, but I’m happy with the result buffer.  Also check out the “Visualize” tab, which will show pairwise plots of your variables (akin to “pairs” in R).

Throw Your Pancakes in the Air!

Once you get the hang of Weka, it is rather empowering to have so many powerful algorithms available at the click of a button!  And instant visualization!  For my first work at Stanford I coded an entire preprocessing / analysis and classifier / validation from scratch in Matlab, so this is, in two words, instant gratification!

A Strategy?

One possible strategy (that seems glaringly obvious now that I’ve given Weka a go) is to use a GUI package like this to very quickly try out a bunch of methods on your data.  Then, once you get a sense of what your data looks like, and which classifiers might be a good fit, then you can go back to statistical powerhouse packages like R where you can really fine tune your analyses.  Also remember that Weka has command line interface for more power in customization.  If you are a fan of python, also give Orange a try.

Looking In

so sharp was the edge of that flesh,
a deep burgandy stained with fermentation
such rush was the pound in my chest
hesitant, and filled with trepidation.

My eyes upon you I started at your base
a thick, and dense, hefty structure
yet somehow it is formidable as a case
without gash, fall, or subtle rupture

I squint glancing upward to your core
protecting my sight from your bold regality
to such a body, many women have adored,
and so many men have reached their fatality

To such a force I will not look,
my eyes skip a blink to move up faster
Feet cold, hair estatic, fingers shook,
of a pungent, earthy spell, you are the castor.

To fast forward time, I rush to your face
hoping to catch a fleeting mercy in your eye
unbelievable how man has formed you in haste
Not a hint of candid, breath, or shy.

Human kind has, and will never conquer you.
Fleshy, putrid, skeething, and filled with lies!
yet every year, you engage us, your creator, in this battle anew.
you, sticky, you malevolent, you unapologetically evil… pumpkin pie!

Cluster Validation

Unsupervised clustering can be tough in situations when we just don’t know “the right number” of clusters.  In toy examples we can sometimes use domain knowledge to push us toward the right answer, but what happens when you really haven’t a clue?  Forget about the number of clusters, how about when I don’t know the algorithm to use?  We’ve talked about using metrics like the Gap Statistic, and sparse K-Means that looks at the within cluster sum of squares for optimization.  These are pretty good.  However, I wanted more.  That’s when I found a package for R called clValid.

Now that I’m post Quals, I can happily delve into work that is a little more applied than theoretical (thank figs!).  First let’s talk generally about different kinds of evaluation metrics, and then let’s try them with some data.  The kinds of evaluation metrics that we will use fall into three categories: internal, stability, and biological.  Actually, stability is a kind of internal, so I’ll talk about it as a subset of internal.

What is internal validation?

Internal validation is the introverted validation method.  We figure out how good the clustering is based on intrinsic properties that don’t go outside of our particular dataset, like compactness, distance between clusters, and how well connected they are.  For example:

• Stability validation:  is like a game of Jenga.  We remove features one at a time from our clustering, and see how it holds up.  For each time that we remove a feature, we look at the average distance between means, the average proportion of non overlap, the Figure of Merit, and the average distance.  For all four of these metrics, we iteratively remove features, and dock points when there is huge change.  A value of 0 would be ideal, meaning that our clustering was stable.  For details, see the link to the clValid documentation above.

• Connectivity: A good cluster should be close to its other cluster members.  That makes sense, right? If there is someone closed to me placed in another cluster, that’s probably not a good clustering.  If there is someone very far from me placed in the same cluster, that doesn’t sound great either.  So, intutively think of connectivity as a number between 0 and infinity that “gets at” how well connected a cluster is.  Specifically, if we have N mysterious lemurs, and are assessing L neighbors, the connectivity is:

meaning that, for each lemur, we look at its distance to each of it’s L neighbors.  For one lemur, i, and his jth nearest neighbor, the stuff in the parentheses is 0 if i and j are in the same cluster, and 1/j otherwise.  In the case that we have a perfect clustering, all nearest neighbors are in the same cluster, and we add up a bunch of zeros.  In the case that nearest neighbors are in different clusters, we add subsequent 1/j, and get some non zero value.  So if you were implementing this, you would basically calculate pairwise distances for all lemurs, N, then iterate through each point, find the closest L lemurs, and come up with a sum that depends on how many of those neighbors are in the same cluster.  Then you add up these sums for all N lemurs, and get the total connectivity value.  0 means awesome, larger numbers mean sadface.

• Compactness:   Within my cluster family, I should be pretty similar to my siblings.  This means that the variance of whatever features define me shouldn’t be very large.  On the other hand, it should be much different from an invidual in a different cluster family.
• Separation:  There should be lots of distance between clusters, whether you look at the distance between centroids, or the distance from the most outside points.
• The Dunn Index:  Since separation decreases as we add more clusters and compactness increases, we have the Dunn Index to nicely combine these two.  The Dunn Index holds to the idea that “a team is only as strong as its weakest member,” and for each cluster, finds the smallest distance to a neighbor cluster, and divides by the greatest distance between any two points in the same cluster.   This value is different from compactness and silhouette because we want to maximize it.  We would want to see a huge distance from other clusters (the numerator) and a tiny tiny distance between the maximum points in the same cluster (the denominator).
• Silhouette Width:  is another nice metric that combines compactness and separation.   Each of our N lemur’s can get a number between 1 (good) and -1 (bad) that represents how well clustered it is.  Specifically, for a point i, we can calculate the average distance it is from its same cluster siblings (ai), and its average distance from all points in the nearest (but different) cluster (bi):

We subtract the average sibling distance from the average foreigner distance, and then divide by whichever value is larger (just to scale it).  In the case that are clustering is perfect, this would mean that the average distance from point i to all its neighbors is zero.  We would then subtract zero from some positive distance value, divide by that same value, and get a result S(i) = 1.  In the equally unlikely and extreme case that our clustering is awful and in fact the average neighboring distance is zero and our siblings have some positive distance, then we wind up subtracting a positive value from zero, dividing by the same positive distance value, and the result is S(i) = -1.  Again, values close to 1 are good, close to -1, not so much.

What is biological validation?

Is my clustering meaningful, biologically?  In the world of informatics, the best example is with microarray data, or anything to do with genes and gene expression.  If we cluster some data based on expression values, we might then use the Gene Ontology (GO) to see if the grouped values (based on similar expression) all fall within some common biological pathway.  For neuroimaging analysis, I can’t say that I have much use for GO.  However, if some day the Allen Brain Atlas has a better sample size for gene expression in the human brain, I might.  For now, let’s say that we have some set of labels for our data that has biological meaning (a type of cell? a type of person? something along those lines.)  Here are common methods for biological validation:

• Biological Homogeneity Index (BHI): how homogenous are our clusters?  Let’s say that we have C clusters, and B classes of biological meaning:

To calculate the Biological Homogenity Index, the result of which will be a value between 0 [no biological meaning] and 1 [homogenous!], we take each cluster (C), and then look at pairwise genes, i and j, within each cluster.  Let’s move from right to left.  The summation on the right is comparing each gene i to each gene j in the same cluster.  The “I” means that we have an indiator function.  This function spits out a 1 in the case that the two genes share any functional class (not necessarily class K), and a 0 if they don’t.  We sum up all of those values, to be multiplied by the summation on the left.  This first summation calculates a value, nk, which is the total number of genes in that cluster that are annotated with B , for some class K.  Intuitively, you can see that if nk==1, or nk==0, the first term is zero, and the BHI is zero as well.  So you would do the above calculation for each of your B classes, and large BHI scores for some class B means that your clustering is annotated in a biologically meaningful way!

• Biological Stability Index (BSI):  Be weary of anything with an acronym that starts with “BS!”  Just kidding.  This is a combined stability and biological validator.  We would want to see data objects with similar biological annotation be consistent in their clustering if we iteratively remove data.   See the documentation linked at the top on page 8 for details.   A value of 1 means that we have stable clusters, and a value of 0 means we do not.

And the algorithms?

I’ve gone over unsupervised algorithms in other posts, so here I will just list what the clValid package offers:

• UPGMA: This is agglomerative hierarchical clustering, bread and butter.
• K-Means! Also bread and butter
• Diana and SOTA: also hierarchical clustering, but divisive (meaning instead of starting with points and merging, we start with a massive blob and split it)
• PAM “Partitioning around medioids” is basically K-means with distance metrics other than Euclidean.  It’s sister package Clara runs PAM in a bootstrappy sort of way on subsets of data.
• Fanny: Fuzzy clustering!
• SOM: self organizing maps!
• Model Based: fit your data to some statistical distribution using the EM (expectation maximization) algorithm.
• SOTA: self organizing trees.

clValid Application - Internal Metrics

Now it’s time to have fun and use this package!  I won’t give you the specifics of my data other than I’m looking at structural metrics to describe brains, and I want to use unsupervised clustering to group similar brains.  If you want to use any of my simple scripts, you can source my R Cloud gist as follows:

source('http://tinyurl.com/vanessaR')

First let’s normalize our data, then look at k-means and hierarchical clustering for a good range of cluster values:

# Normalize data
x = as.matrix(normalize(area.lh))

library(‘clValid’) clusty &amp;amp;amp;amp;amp;amp;amp;lt;- clValid(x, 2:20, clMethods=c(“hierarchical”,”kmeans”,”pam”),validation=”internal”,neighbSize=50) summary(clusty) plot(clusty) </code> </pre>

clValid gives us each metric for each clustering, and then reports the optimal values.  I ran this for different numbers of clusters, and consistently saw 2 as being the most prevalent, except for when using k-means:

I tried increasing the number of clusters to 20+, and tended to see the metrics drop.  Let’s take a look at 2 to 50 clusters:

Connectivity

Remember, this should be minimized.

Dunn

This should be maximized!

Silhouette

Maximized! (up to 1)

So what are some issues here?  It looks like the data is somewhat “clustery” when we define two groups.  However, a main is feature selection.  I haven’t done any at all :).  Just for curiosities sake, let’s look at the dendrogram before moving on to testing stability metrics:

It certainly makes sense that we see the best metrics for two clusters.  The numbers correspond to a biological label, and now we would want to see if there is a clustering that better separates these labels.  It’s hard to tell from the picture - my best guess is that it looks kind of random.  Let’s first look briefly at stability metrics.

clValid Application - Stability Metrics

# Now validate stability
clusty <- clValid(x, 2:6, clMethods=c("hierarchical","kmeans","pam"),validation="stability")
optimalScores(clusty)

Remember, we are validating a clustering based on how much it changes when we remove data.  This took quite a bit of time to run, so I only evaluated between 2 and 6 clusters.  I would guess that kmeans would show “consistent improvement” with larger values of K (of course if we assigned each point to its own cluster we’d have perfect clustering, right?) and for hierarchical, as the tree above shows, our best clustering is a low value around 2 or 3.  Let’s try some biological validation.  This is actually what I need to figure out how to do for my research!

clValid Application - Biological Metrics

What I really want is actually to evaluate clustering based on biology.  I have separate labels that describe these brains, and I would want to see that it’s more likely to find similar labels in a cluster than not.  I really should do feature selection first, but I’ll give this a go now just to figure out how to do it.  Note that, to simplify things, I just used two annotations to distinguish two different classes, and the annotation variable (rx.bin) is a list, which the function converts into a matrix format.

# Validate biologically - first create two labels based on Rx

rx.bin = rx.filt
rx.bin[which(rx.bin %in% c(0,1))] = 1
rx.bin[which(rx.bin %in% c(2,3,4,5))] = 0

# Now stick the binary labels onto our data
annot <- tapply(rownames(x.filt),rx.bin, c)
bio <- clValid(x.filt, 2:20, clMethods=c("hierarchical","kmeans","pam"),validation="biological", annotation=annot)
optimalScores(bio)

And as you see above, we can use the optimalScores() method instead of summary() to see the best of the bunch:

Remember that, for each of these, the result is a value between 0 and 1, with 1 indicating more biologically homogenous (BHI) and more stable (BSI).  This says that, based on our labels, there isn’t that much homogeneity, which we could have guessed from looking at the tree.  But it’s not so terrible - I tried running this with a random shuffling of the labels, and got values pitifully close to zero.

Summary

Firstly, learning this stuff is awesome.  I have a gut feeling that there is signal in this data, and it’s on me to refine that signal.  What I haven’t revealed is that this data is only a small sample of the number of morphometry metrics that I have derived, and the labels are sort of bad as well (I could go on a rant about this particular set of labels, but I won’t :)).  Further, we have done absolutely no feature selection!  However, armed with the knowledge of how to evaluate these kinds of clustering, I can now dig deeper into my data - first doing feature selection across a much larger set of metrics, and then trying biological validation using many different sets of labels.  Most of my labels are more akin to expression values than binary objects, so I’ll need to think about how to best represent them for this goal.  I have some other work to do today, so I’ll leave this for next time.  Until then, stick a fork in me, I’m Dunn! :)

Functional Brain Network Visualization

Now that we have (finally) come up with a correlation matrix to describe the relationship of voxels across the brain, let’s explore some simple methods from graph theory.  To make this analysis somewhat more simple, I’ve thresholded my brain network to only include the most highly connected regions, those with correlation values greater than .9.  Here is a visualization of the voxel pairs that we will use in the sparse correlation matrix:

It most definitely is the case that most of these voxels appear to be neighbors, however that will make it more interesting to find the links that are in different regions.  Here is the corresponding spatial map for this level of threshold:

I was first curious about the distribution of voxels in each region, and so I returned to the AAL atlas to get a count.  Out of 9671 voxels, the left precuneus dominates, but it’s not as crazy large as the chart makes it out to be, only 657 voxels.  To give this some perspective, the amygdala, which is a rather small area, is about 242 voxels.  The precuneus is a region posterior to somatosensory cortex, and anterior to occipital lobe (yes, this makes it a part of the parietal lobe) associated with visuospatial processing, consciousness, and episodic memory.

At this point I started looking into functions that Matlab has to work with graphs, and hit another road block.  They really aren’t suited for data of this size.  Actually, this dataset doesn’t seem unrealistically large to me in context of genetic network analysis.  It was clear that I would need different software, and so my first test was Cytoscape.  I exported my nodes, exported the labels for the regions, as well as the edges (weights) between them.  Granted that I know nothing about this program I don’t have any prowess in using is, but I was able to color nodes by region, and adjust edges based on the weight value.  Largely, having every voxel as a node was just too much:

The most that I could learn from this “visualization” was that if I viewed my data based on the region attribute, I could see that there were local (regional) networks, and then inter-regional ones.  Another downfall was that the software interpreted the ordering of my edges as directional, which isn’t the case.  However, I’m not quite ready to give up!  I want a visualization that is more humanly interpretable.  I decided to go back to the raw data and calculate, for each region, the average intra-regional correlation, and the average inter-regional correlations (the average pairwise correlations to all other regions).  I wanted one node per region, and I wanted the size of the node to represent the intra-regional connectivity, and the edges to represent the inter-regional connectivity.

There we go!  The “organic layout” graph above represents connectivity between 116 distinct brain regions, with the size of the node representing the intra-regional connectivity, and the thickness of the edge the inter-regional connectivity.  The lack of huge variance in the node and edge sizes is due to the fact that the values are thresholded at .9 and above to begin with.  The red edges represent connections between the right and left amygdala and other brain areas.  This was definitely fun - me using Cytoscape is akin to a monkey wandering around an outlet mall looking for the candy dispenser that has the banana candy in it.  I learned that this software is probably best for higher level representations of networks, and it doesn’t do too well for very large data, so I might come back to it only if I have that kind of representation in my research.  If you look at the spatial map above, this just wasn’t that much data in the scope of the entire brain!  All in all, I met my goal, and so I’m happy with that visualization, for now.

Tracing a Functional Brain Network

I’m reading about different ways to understand and process functional data, and so methods from graph theory serve as good candidates.  I’m excited about these methods simply because I’ve never tried them out before.

Creating the Graph

Assess Correlations between points and threshold to create a graph

We are starting with a graph, meaning that we have accessed the connectivity (correlation or some similarity metric) between all pairwise voxels in a brain, and then applied a threshold to leave only the more highly connected voxels.  If a connection between two voxels falls below the threshold, the “edge” is broken, and if the value is above the threshold, we maintain the edge. To explore these different kinds of connectivity, let’s again work with actual functional data.  First, let’s read in the data and flatten it into a 2D matrix (Yes, I am modifying the path and files names for the example):

code

At this point I would want to make a correlation matrix like this:

code

but of course I ran out of memory!  I then queried my friend Google for some data structure in Matlab for sparse matrices, and found it, the function “sparse” of course!  Instead of creating the entire correlation matrix and then thresholding, what we can do is find the indices for correlations already above some threshold, and then plop these values into a sparse matrix.  This “sparse” function takes as input a vector of indices and a vector of values, and you create the matrix in one call.   So, we need to create these two vectors, and just hope that there aren’t enough values to have memory issues:

code

Seems like a good idea, right?  Don’t do it!  The above will run for days, if it even finishes at all.  Here is where I ran into a conundrum.  How have other people done this?  Is it really impossible to create a voxelwise graph for one person’s brain?  I first explored tricks in Matlab to use matrix operations to efficiently calculate my values (think arrayfun, matfun, etc.)  This didn’t work.  I then learned about a function called bigcor in R from a colleague, and exported my data to try that out.  Even my data was too big for it, and I had to split it up into a tiny piece (20,000 / 520,000 voxels) and then it took quite some time to work on the piece.

A function for sparse matrices in Matlab? Not yet.

If the best that I could do was a piecewise function in R, then I figured that I might as well write my own function in Matlab.  I knew that I would just need to break the data into pieces, calculate the correlation matrix for the piece, and then save indices relevant to the original data size with the corresponding correlation value.  And I would probably want to save results as I went to not run out of memory with long lists of indices on top of the original data and correlation matrix.  I’m squoozy to admit that I spent most of a weekend on said function.  I’m not sharing it here because, while it technically works, the run-time is just not feasible, and so after spending the time, I decided that I needed to pursue a more clever method for defining a local brain network.

Introducing, Mr. Voxel!

This exploration began with just one voxel.  If I am going to create a method for tracing some functional network, I need to have a basic understanding of how one voxel is connected to the rest of the brain.  Introducing, Mr. Voxel, who is seeded in the right amygdala.  My first question was, how does Mr. Voxel function with all the voxels in the rest of the brain, and his neighboring voxels?

The plot to the left shows correlations between Mr. Voxel and the other 510,340 voxels in the brain.  The plot to the right shows correlations between Mr. Voxel and his neighbors, defined by also being in the right amydala region of the AAL atlas.  It seems logical that neighboring voxels would have more similar timecourses than far away ones.  However my next question was, where are the most highly correlated voxels located?  I chose a threshold of .5 because .55 / .6 seemed to be the tipping point, when we jumped from 16 and 22 voxels, respectively, up to 162.  Here is the breakdown for the top 162 voxels:

code

and the distribution of the correlation values themselves:

But we can do better!  Let’s take a look at the spatial map for these voxels:

I’m quite happy with this result.  I would want to see the most highly connected voxels being the neighboring ones in the amygdala, and then some friends in frontal cortex and hippocampus.  Now what?

A function to generate the graph of a local network

What I really had wanted to do was generate a simple network so that I could test different graph metrics, and so I decided that it would make sense to start at a seed voxel, and trace a network around the brain, adding voxels to some queue that are above some threshold to expand the network.   Since this could get unwieldy rather quickly, I decided that my stopping conditions would be either an empty queue (unlikely!), or visiting all 116 unique regions of the AAL atlas.  For each iteration, I would take the top value off of the queue, find the most highly correlated voxels, and save them to my network.  I would then only add voxels to the queue that came from novel regions.  I know that this is a biased approach for whatever regional voxel gets lucky enough to be added first, and even more biased based on what I choose for an initial seed.  For this early testing I’m content with that.  I will later think about more sophisticated methods for adding and choosing voxels off of the queue.  Whatever strategy that I choose, there probably isn’t a right answer, and what is important is only to be consistent with the method between people.

Queue Popping Method Development

First, let’s look at the growth of the queue.  The plot below shows the number of voxels in the queue at each iteration:

Based on only going through 158 iterations and visiting 101 AAL regions in those iterations, I realized that most of my queue wasn’t even going to be used.  I need to rethink my queue popping strategy.  Now let’s take a look at the breakdown of the old queue.  Out of a final total of 15120 contenders, there are in fact only 5665 unique values, and they are spread across the entire AAL atlas:

We could either limit the voxels that we put on the queue to begin with, or we could develop a strategy that takes this distribution, and the regions that we’ve already visited, into account.  On the one hand, we want to visit a region that has more representation first, but we don’t want to keep visiting the same popular regions in the network over and over again.  Stepping back and thinking about this, I would want to do something similar to what  is done in vector quantization.  I want a vector of sensitivity values that bias our choice toward regions that haven’t been selected, and I also want to take into account the number of voxels that are in the queue for that region.  I modified the script to take these two things into account, and used it to generate my first local network!  Keep in mind that this network is an undirected graph because we can’t say if a connection between voxels i and j is from i to j, or j to i.  I finished with a list of links, and a list of values to describe those links (the weights).  I then (finally) used Matlab’s sparse function to create the adjacency matrix for my graph:

code

The above is saying to create a sparse matrix with x values from links(:,1), y values from links(:,2), fill them in with ones because there is one link between each set of nodes, and make it a square matrix sized as the original number of voxels (that Matlab could not handle as a non-sparse matrix).  After this adjacency matrix was created (albeit in like, two seconds!), I used the “spy” function to look at the indices of this beast matrix that are included in the graph.  This definitely isn’t everyone, but it’s a good sampling across the entire matrix, and I’m pretty happy that I was able to pull this off.  The stripes of emptiness are more likely to be area outside of the brain than “missed” voxels.  Remember that this isn’t the graph itself, just the indices of the members, and the correlation threshold is .55, which could easily be increased.

Trying to visualize these voxels, spatially, in Matlab is not a good idea.  Instead, let’s write the included voxel coordinates to file, and overlay on an anatomical image:

My instincts were correct that I got most of the brain, and for a first go at this, I am pretty pleased!  The running time wasn’t ridiculous, and we get coverage of most of the brain’s gray matter.  In fact, I think that it’s even too much, and I’m going to up the threshold.  For my next post, I will increase the threshold to a much higher value (.9?) and see if I can visualize this network as a graph.  My goal is to get a sense if using this kind of graphing software for visualization makes sense for functional MRI data.

Exploring Raw Functional MRI

I’m curious if using a mean timecourse to represent a region is a good idea or not.  What I did is, for a functional timeseries with 140 timepoints, I wrote a script to mask the data for a region of interest, and then for the voxels within each region, plot all of the normalized individual timecourses (blue) and compare against the mean timecourse (in red).  These are essentially Z values, meaning that we have subtracted the mean and divided by the standard deviation.

1) Does a mean timecourse do a good job to represent a large region?

Here we have the collection of timecourses for the first region of the AAL atlas, the Precentral gyrus, on the left.  The precentral gyrus is home to motor cortex:

Schmogley!  I suppose you could argue that the mean timecourse gets at the “general” shape, but this just seems like a bad idea.  Although to be fair, this is a rather large region.  You are looking at just about 12,000 voxels.

2) Does a mean timecourse do a good job to represent a small(er) region?

Let’s try a smaller region, like the right amygdala.  This is about 1000 voxels:

It’s slightly better looking, but I’m still thinking that this isn’t a great idea.

3) Assessing timecourse similarity

Let’s assess this properly and calculate a distance matrix  The indices of this matrix will represent the similarity between timecourse i and j, so when i==j, we would see a distance of 0 meaning that they are exactly the same.  The larger the value gets, the more different.  So we should see values of 0 along the diagonal (when i==j)) and I’d also suspect that neighboring voxels are firing together:

What we see here is that there are most definitely voxels that share a similar timecourse (blue), and then there are a small number of voxels that are different.  I’d like to think that this is because of actual biological differences, but I’m also thinking that it’s likely to be noise.  The amygdala is situated rather low in the head, and it tends to be victim of what we call signal dropout.  Namely, that it’s possible to lose signal in some of the timepoints.  Or be subject to noise.

4) Clustering Distance Matrix to find “the right” groups?

I have a good idea… let’s try clustering this distance matrix, and then looking at the timeseries for each of the clusters.  This is pretty easy, because the x and y labels correspond to the voxel index.  From the above I’d guess three clusters, but let’s do a dendrogram first to see if this is a good idea.

Yes, I think so.  Let’s try 3 clusters, and plot the timeseries for each of our three.

5) Mean timecourses for clustered groups of voxels

I decided to try for three clusters, and then six.  While there is slight improvement in the mean representing the group, it still looks kind of bad to me.

and six groups…

If these plots looked better, my next step would have been to assess the spatial location of the voxels.  But I’m not convinced that these groups are very good.  And here we have a conundrum!  On the one hand, we want to use more abstract (regional) features, because if we really do look at the data on the level of every single voxel, that is prime to overfitting our data.  We aren’t going to find interesting patterns that way that could be extended beyond our training set.  On the other hand, if we zoom out too much, it’s just a mess.

6) We can’t make assumptions about similar function based on spatial location

In this exploration I’ve shown an important idea.  We can’t make strong assumptions about function based on spatial location.  Yes, it’s probably true that neighboring voxels share similar timecourses (reminds me of a nice quote from NBIO 206) but we would be silly to assess for similar firing within one brain region.  It’s likely that if we zoom out our distance matrix, there would be voxels in other parts of the brain with more similar timecourses to specific voxels in the amygdala than other voxels within the amygdala.  This is exactly why many approaches calculate whole brain voxelwise similarity metrics, and then threshold the matrix (keeping only the strongest connections) to create a graph.  This graph represents a connectivity matrix, and “gets at” what the buzz word “the human connectome” represents (on the functional side of things, note that you can also look at a structural connectome, representing areas that have physical neuron highways between them).  Since this would be a huge matrix, this is why researchers either set “seed” points (voxels they have reason to believe are the best or most important), or use a mean timecourse to represent some larger set of voxels before creating this graph of connections.

7) So how can I make more “abstract” features for functional data?

This is why, for functional data, I prefer methods like ICA that can decompose the brain into some set of N independent signals, and their timecourses, not making any pre-conceived assumptions about spatial location of voxels (other than assuming independence).  Since I’d like to transform my functional data into some set of meaningful features to combine with my structural data and predict things like disorder type (probably won’t be good models) or behavioral traits (a better idea), I need to think about how I want to do this.  I don’t think that I expected to learn from this simple investigation that it would be a good idea to extract features about the signal of mean timecourses, so this introduces opportunity for creative thinking.  But I kind of want to work on something else for now, so I’ll save that for another time!

Exploring Raw Structural MRI

I’m happy to report that I’ve passed my Qualifying exam, and so the past week has largely been filled with what I consider “fun” work, e.g., playing with data with no pre-defined goal or purpose, and reading about methods just for the heck of it.  Before I delve into some basic data exploration I want to recommend two things.  1) Andrew Ng’s Deep Learning tutorial as a good place to start learning about how to implement such algorithms, and 2) the radiolab podcast as just a wonderful show to learn about unexpected topics in the frame of narrative intermixed with interview and humor.

Voxel Based Morphometry to assess Differences in Brain Structure

The commonly used method to derive maps of gray, white, and csf volumes for each little cube (called a voxel) in the human brain is called Voxel Based Morphometry.  This method starts with a structural scan (a T1 image), and some of the outputs include maps of volumes, where each voxel numerical value represents the amount of the tissue type within the voxel in cubic mm.  The maps are also normalized to a standard template, so you could do statistical tests with a group of individuals to assess for significant differences in the volumes of a particular matter type.  And to answer the questions that you are thinking, yes we must correct for multiple comparisons because we are testing a hypothesis at each voxel, and yes, people have differently shaped brains, and so the normalized maps are modulated to account for whatever smooshing and scaling was done to fit the template.  This method is the bread and butter, or at least a starting point, for most structural analysis.

Distribution of Gray, White, and CSF Matter in the Human Brain

I’ve used this method many times before, and mostly that meant building a solid pipeline with careful preprocessing, registration checking, and derivation of the resulting maps for my data.  What I haven’t done, and have been dying to do, is just playing around with the data.  I’m sure that these simple questions were investigated long ago and so no one bothers to ask them anymore, but hey, I want to ask!

1.  What is the distribution of each matter type in the human brain?

I really just wanted to plot each matter type, and compare, and so I did.  The charts below are reading in each of the maps, and then plotting a histogram for only nonzero voxels, with 100 bins:

From this we see that most of the brain is gray matter.  But I kind of wanted to get a sense of the distribution of different matter types, on a regional basis.

2.  How does the composition of gray, white, and csf vary by region?

So I registered the AAL atlas template (consisting of 116 regions) to my data, and then calculated a mean volume for each region, and then plot them in 3D.  (Just as a side note, this data is registered to one of the icbm templates, so getting the AAL atlas in the space of my images meant registering to that).  You probably need to click on this to see the larger version:

Most voxels are, as you would guess, a mixed bag of tissue types.  It’s cool that, depending on the partition of the cerebellum we are looking at, there is a pretty big range of gray matter composition.  Actually, the plot is kind of misleading because it doesn’t show the range of white matter.  Let’s get rid of csf and just look at gray vs. white matter:

Remember that these are mean regional values, which is why the range looks smaller than before.  We again see the nice range of gray matter in the cerebellum, and it makes sense that there is a sort of inverse relationship between the two.  But how does this compare between people?

3.  How does the composition of gray, white, and csf vary by region for many people?

Let’s take a look at the fuzzy chart that we get when we plot ll 116 regions for… 55 brains!

It looks like a sneeze cloud, and given the huge number of regions, we only see some clustering in the outskirt regions.

4.  How does composition (represented by percentages, and not volumes)  vary by region?

I have a better idea.  Instead of plotting the matter amount in cubic mm, let’s calculate and plot the percentage of matter in each region.  I think we will see a nicer clustering:

We sure do!  it’s still largely a mixed bag, but this rescales it to give better defined clusters.  For each region (distinct colors above) the percentage of white + gray + csf (not shown) must sum to 1.  It’s interesting to see that there is nice variation within each region, depending on the person.  Could we predict the region based on these values?

5.  Can mean tissue composition distinguish regions?

Based on the pictures above, I would guess that the answer is no for most of the data.  But I thought I’d give it a try anyway!  I used linear discriminant analysis to build a classifier to predict region label based on mean regional values for tissue composition.  I hypothesized that using the percentage of each matter type (the chart directly above) would do slightly better than using raw, modulated volumes (two charts up), and that both (given the huge overlap that we see) would do rather poorly.  Glancing at the data above, I decided to use linear instead of quadratic discriminant analysis because I think it’s safe to assume the same covariance matrix.  Since I don’t have a separate test dataset (and deriving one would take many hours of processing and space on my computer that I just don’t have), I decided to just use leave one out cross validation, make a prediction for each person’s set of three mean values (corresponding to one label out of 116) to calculate an overall accuracy.  116 labels is a lot.  And there is a lot of overlap.  Still, I was surprised that for the above chart, the accuracy was 31%.  Each region has 55 sets of values, and there are 116 regions, so actually I think that’s pretty good given the sillyness of this problem of predicting brain region based on percentage matter composition.  Who were our top performers?  The values here are the percentage that we got right:

code

Wait a minute, in using these 116 AAL labels, we have separate labels for the same region on the left and right hemispheres of the brain, as well as different “sub” regions.  What if we do away with this detail and instead use the same label for regions on corresponding sides of the brain, as well as subregions?  Yeah, let’s try that! 😀  Woohoo! Accuracy increases to… a still dismal 37%.  But it increases!  Here is what the data now look like:

I still contend that is pretty good.  What if we go up another degree and combine subregions?  Here is what it looks like for 30 regions:

Oh dear, this isn’t going to be good - in combining all the different parts of the frontal and parietal lobes, for example, we’ve actually lost information in combining regions that do have different matter compositions, and telling our learning algorithm that they are the same.  In fact, accuracy drops to 8%.  Oh dear.

6.  Can tissue composition distinguish disorder type?

It’s not so useful to predict brain region based on matter composition.  A better question might be something about the people.  How about a disorder?  I will reveal to you that this data is a subset of NDAR, and so this is a mixed cohort of ASD (autism spectrum disorder) and healthy controls.  While we know that ASD have significantly larger brains, I don’t think that we would find meaningful differences with regard to the compositions, represented by percentages.  Still, I’d like to try.  (Going back to the original 116 labels) first I visualized each region, and added a label to distinguish disorder type.  Zero (0) == healthy control, and 1, 2, and 3 correspond to different severity of ASD.  Here, for example, is what most of these plots looked like:

I’m not sure how well we could do using these features to predict disorder… it’s hard to tell from looking at the plots individually.  I actually think it would be more meaningful to predict specific behavioral traits (e.g., anxiety, impulsivity, that sort of thing) because I’m not a huge fan of the DSM labels to begin with.  I want to try building a classifier, but first I want to explore functional data.  From the investigation above we can see that there is variation in volumes / percentages, but the question is now if this variation is meaningful.  With this in mind, each of my values for gray, white, and csf for each region becomes a unique feature.  But what will I use for functional data features?  What is normally done in region based analyses is to extract an average timeseries across the region.  But is that a good idea?  Does a mean timeseries truly reflect the entire region?  Methinks that another investigation is in order before making this classifier, and I’ll also put that investigation in its own post.  Yes, I do have resting BOLD data for these individuals, and yes I’ve already done all the preprocessing to have nice filtered, normalized brains over time (what else is a girl supposed to do with a long weekend? :P)

Just kidding, don’t answer that!

I will do some functional investigation, and then we will combine these two feature sets to try building a bunch of different classifiers.  Cool cool!

Brain Podcast with Temple Grandin

This is an episode of the Brain Podcast that interviews Temple Grandin, and it’s good enough that I want to share:

Interview: Temple Grandin

I listened to it a few days ago, but the points that stuck out as interesting to me were:

• Dr. Grandin says that ASD is heterogenous in almost every regard except for one common factor, social deficits
• She thinks a logical way to diagnose would be using fMRI, specifically looking at these social networks, because ASD is different in every other regard
• She thinks that an approach that uses specific traits (eg, sensitivity to touch, sound, yes or no) over clumping ASD into one group makes most sense (I agree!)

Dr. Grandin also gives very interesting details about her personal experiences, research, and perception of the world.  It’s a good talk, and you should listen.

Dual Regression to Compare Functional Brain Networks

I want to talk about a method that is quite popular with functional network analysis, namely to define functional networks for a group of people, and then go back and identify the same (unique) network for an individual.  This technique is called dual regression, and if you want to do higher level analysis with this data, it’s important to understand how it works, and the resulting spatial maps.  These beautiful pictures come by way of a poster from Christian Beckmann, who has done quite a bit of work with FSL / Melodic / ICA.

Define Group Networks

First, we use independent component analysis to define group networks.  We do this the same way as we would for an individual network, except our “observed data” (X) that we decompose into a matrix of weights X spatial maps is actually many individuals’ timeseries, stacked on top of one another:

If you use FSL, this technique is called “multisession temporal concatenation.”  I’m not a fan of using the GUI (especially for resting state because it doesn’t have bandpass filtering, forces you to do some other filtering that isn’t desired, forces doing individual ICA first (takes forever!), and also forces registration), so I typically use the melodic utility command line.  I’ll do another post about the specific commands, etc.

Why wouldn’t we just stop here? Because the group maps, by definition, lose meaningful detail on the level of the individual.  If you have group decomposition for two different groups you could identify equivalent networks with some template matching approach (or just visually) and then assess for differences, but at best that would be a very rough analysis.  This is where dual regression comes in.

Dual Regression to Define Individual Components from Group Components

We start with a set of group components (the middle matrix), and our goal is to use these maps with each individual subject data (the first matrix) to define, first, timecourses, and then individual level spatial maps.  The picture below shows how this is done.  If X = group maps X timecourses,

How does this make sense? Let’s think about a simple case.  The value in row 1, column 1, of the first matrix (X) is produced by taking the first row of the middle matrix (G), and transposing it (the dot product) with the first column of the unknown matrix (I).  For example:

X11 = G11I11 + G12I21 + … + G1n * In1

We know X11, and we know each of the G* values, so it becomes a simple case of solving for the “coefficients,” I.  It’s a linear equation.  We can extend this to the entire matrix, and we would want to solve for the matrix I in this equation:

X = G * I

I tried out a simple example of this in Matlab, and I just used the linsolve function:

code

with a simply defined X and G, to produce a matrix I.  I then multipled G by I to affirm that I reproduced my X, and I did.  So, by doing this and solving for I, this matrix I represents the timecourses for an individual person relevant to the group spatial map.  In many implementations, we then normalize these timecourses to unit variance, so we can compare between them.  We can now use these individual timecourses to define the individual’s spatial maps:

Namely, we use the timecourses as temporal regressors in a General Linear Model (GLM) to come up with the spatial maps.  We can then do permutation testing to assess for differences between groups, or do some higher level analysis using the spatial maps and timecourses.

Visualize Dual Regression Results

I wrote a script to create an incredibly simple web report visualization of the corrected and thresholded dual regression maps, one for each contrast.  You can see some sample output here, and the scripts are here.

Visual: Should I use a linear model?

I’ve read about this trick in two places, as a way to determine if the choice of a linear model for your data is a good one.  You can plot the residuals (the squared error terms) against each of the corresponding predicted values (the Y’s), and if a linear fit is not good, you will see funky shapes!  For example, (another fantastic graphic from ESL with Applications in R):

The plot on the right shows that a linear model is not a good fit to the data, because there is a strong pattern that indicates non-linearity.  When we transform some of the variables (for example, squaring one of them), this pattern goes away (the image on the right).  Transforming your variables is another trick that we use to use linear regression to fit polynomial-looking data.  Very cool!  Plotting the residuals like this is also a good strategy to find outliers.  While an outlier may not change your model fit drastically, it can drastically change the R (squared) statistic, so you should keep watch!  In this case, we can also calculate the studentized residuals, which basically means dividing by the standard deviation, and then plotting that.  If there is a studentized residual greater then about 3, spidey sense says that it is probably an outlier.

Correlation

Correlation is a measure of the extent to which two variables change together.  A positive correlation means that when we increase one variable, the other increases as well.  It also means that when we decrease one variable, the other decreases as well.  We are moving in the same direction!  A negative correlation means that when we change one variable, the other moves in the opposite direction.  A correlation of zero means that the variables are independent - changing one doesn’t influence the other at all.

How to calculate correlation?

Let’s say that we have two variables, x and y.  Correlation is basically the covariance(x,y) divided by the  standard deviation(x) multiplied by the standard deviation(y).  It’s easy to remember because the equation for covariance and standard deviation are pretty much the same except for the variables that you plug in.  To calculate standard deviation, we subtract the mean from each value of x or y, square those values, add them up, and take the square route. You can see that we do this calculation for both x and y on the bottom of the fraction below.  Covariance (on the top!) is exactly the same except we subtract each of x and y from their respective means, and square those two results.  We don’t take the square route to calculate covariance (see my post comparing the two):

Again, the top of this equation is covariance(x,y), and the bottom is standard deviation (x) multiplied by standard deviation (y).  I think that this makes sense, because if x and y were exactly the same, the denominator would simplify to be the same as the numerator, and we would get Cor(X,Y) = 1.

Correlation is related to R (squared) statistic!

One cool thing that I learned recently is that squared correlation is equal to the R (squared) statistic in the case of two variables, x and y!  I think that also means that we could take the square route of the R (squared) statistic and get the correlation.  This means that we could also use correlation as a metric for goodness of fit.  This works nicely in the case of our two variables, however since correlation is only defined to be between these two variables, we can’t use it as this metric for multivariate regression.  In this case, Mr. R (squared) wins.

R (squared) Statistic

I remember making plots in middle and high school, and this curious r-squared statistic told me something about how well my data fit some regression plot.  I had no clue where this value came from, but I noticed that it ranged between 0 and 1, and values closer to 1 were indeed better.

The r-squared statistic is a measure of fit.  Further, it is intuitive because it tells us the proportion of variance of the data explained by our model.  Thus, a value of 1 means that we explain 100% of the variance, and let’s just hope that we don’t see any r-squared values == 0.

How to calculate Mr. R (squared)

To calculate the r-squared statistic, we need to know the residual sum of squares (RSS), and the total sum of squares (TSS).  The TSS measure the variance in the response of Y (the y bar is representative of the mean of Y), and the RSS measures the variance in our predictions (y hat), or the variance that is not explained by our model.  Each is defined as follows:

In this regard, if we were to subtract the RSS from TSS (TSS - RSS) we would get the amount of variance that is explained by our model.  Then if we divide by the TSS, we get variance explained by the model as a percentage of total variance, which is what we want:

Now with this r-squared statistic, since it is normalized, we can compare between different models and data.  Cool!  So what does it mean if the percentage of the variability of Y as explained by X is really low?  It means that the regression model isn’t good to fit the data.  Try something else!

A Note of Caution…

Be cautious about using this statistic to do any form of feature selection (i.e., don’t!) because when you add variables to the model, Mr. R (squared) will always increase.  However, you could look at the degree of the increase.  For example, if a variable adds little to the model, the increase will be tiny, as opposed to a variable that makes it much better.

What is Standard Error?

Let’s say that I have a huge file cabinet filled with pasta (choose your favorite kind from “the Plethora of Pasta Permutations”) and I want to know the volume of each piece (let’s say there is a contest to guess how many pieces of uncooked pasta will fill a pot perfectly).  For example, how about some hello kitty pasta?:

There are different shapes, and variance within one shape type, and there is no way that I would want to cook and take the volume of every single piece, then average to find the true mean, but I could take a sample of pasta, find the average volume of my sample, and use that to estimate some “true” mean volume.

Standard Error tells me how good of an estimate my sample is

The standard error, or standard deviation, gives us a sense of how far off my sample mean is from the true mean.  If my sampling is unbiased, then the sample could be either a slight overestimate, or underestimate.  If my sample is biased (for example, if I had some kind of hook that more easily grabbed a hello kitty and not a flower) then my mean volume estimates would probably be too big.  Let’s assume my sample is unbiased.  To calculate the standard deviation (s), I would first calculate the mean volume (x bar), subtract it from each sample volume, square that result, and add up all the squares for my entire sample.  Since we have a sample, I would then divide by N-1, and taking the square route would solve for the standard error:

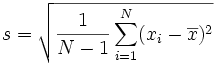
This value represents how far off any random sample is likely to be from the mean.  Note that we divide by N-1 because we are taking a sample.  If we are calculating the standard error for the entire population, we just want to divide by N, and note how the variable we use to represent this value has changed from s:

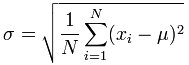
If we don’t take the square route, then we are just solving for the variance, and so we can say that variance is equal to the standard error (above) squared:

We typically start with variance, actually, and then just take the square route to get the standard error.  What’s the difference between the two?

Standard error is (sort of) intuitive, variance is less so

I (think) the reason that we have standard error (taking the square route of variance) is because it is more intuitive.  Since variance is an average of squared values, it doesn’t make much sense in the context of our data’s units.  However, when we “undo” the squaring by taking the square route, we get a value that is more easily to relate to our data units.  This is why I would be interesting in calculating the standard deviation for my sample of pasta.  It would give me a good estimate of the average volume that I’m off by when I do a sample, which might give me insight to how many samples I should take to get a good estimate.

How is this useful in machine learning?

In infinite ways!  However I will just give one example, with linear regression.  If we are taking n samples of data to fit a linear model by finding the least sum of squared error, for each time that we take a sample, we would come up with some estimated beta value (B1).  We would then get a distribution of B1 values, and we would want to know “what is the chance that the “true” B1 value is in this distribution? “ We would want to calculate a 95% confidence interval, and we would do this with the standard error:

Basically, the equation above says that we define a range that is 2 X the standard error of our estimate above and below it.  This means that 95% of the samples that we generate will have the true value in this interval, and the other 5% are type I error.

We can also use the standard error to calculate a T-statistic, or the number of standard deviations that an estimate is from the sample mean.  If we are assessing if a particular sample is “significantly different” then we would want to know if it falls within this 95% confidence interval or not.  If we find that our sample is in the 5 percent of values that are NOT 95% likely to contain the true population sample mean, then we reject the null hypothesis and call the sample significant.  We calculate a T-statistic by subtracting the mean, and dividing by the standard error.

If my memory serves me correctly, a t-statistic of +/-1.96 is a good estimate of the 95% confidence interval for normalized data with mean zero.

Visual: How Sampling can Approximate a True Relationship

We know from central limit theorem and the law of large numbers that when we take a bunch of random samples from some unknown distribution, and then look at the distribution of sample means, as our number of samples goes to infinity the distribution look normal, and the mean of this normal distribution approaches the expected value of the “true” mean of the distribution. My favorite explanation of this phenomenon comes from Sal Khan at the Khan Academy, and I just stumbled on a nice plot that shows how the same idea is true with regard to linear regression.

How Sampling can Approximate a True Relationship: Linear Regression

This plot is from ESL with Applications in R.  The plot on the left shows our data, with the red line representing the “true” linear relationship (for the entire population), and the blue line representing an approximation made with a sample by way of minimizing the sum of squared errors.  We can see that, although the two lines aren’t exact, the estimation using the sample isn’t so far off.

The plot on the right again shows our population “true” relationship (red), and the sample estimate (dark blue), however now we have added a bunch of estimates from many random samples (the light blue lines).  Here is the super cool part - we can see that if we take an average of these random sample lines, we come quite close to the true relationship, the red line!  I (think) this is a good example of something akin to central limit theorum applied to a learning algorithm.

Visual: Plotting Model Complexity vs. Error

I recently purchased the new Elements of Statistical Learning (with Applications in R) by Witten, Hastie, Tibshirani, and James, and am completely taken with the beautiful plots in this book.  Of course I won’t redistribute my copy, and I’m not sure if I’m allowed to do this, but I want to write short “Visual” posts that show and explain a plot.  I’m a very visual learner, so these have been very helpful for me.

Plotting Model Complexity vs Error - KNN

When we talk about the complexity of a model, we might be getting at the number of indicator variables (our x’s) used to build the model, such as with linear regression.  A higher number == more complex model, and the complexity of the model has a lot to say about generalizability error, or how well our model performs when extended to other data.  We reviewed the idea of the mean squared error being represented as a sum of squared bias and variance, and generally when a model is very complex (low bias and high variance) this could lead to overfitting (high test error, low training error), represented by this plot:

Error is on y, and complexity on x.  When we go past the “sweet spot” we are overfitting  because test error starts to go up as training goes down.  It wasn’t completely clear to me how I could think about model complexity with regard to knn, until I found this beautiful plot:

Why of course! We model the complexity of KNN with 1/K.  This means that when K=1 (far right side), our model is going to perform very well on training data (blue line), and not so well with different test data (orange line).  We are overfitting, and likely have low error due to bias and high error due to variance.  On the other hand, when K is very large (left side of plot), we don’t do well in either case.  You can imagine the extreme case when K = size of data, we just have a “majority rules” classifier that assigns the majority class to everyone.  This means that we have high error due to bias (a bad model!) and low error due to variance (because when we change our data, the predictions don’t change much.)

Optimization Functions

I wanted to compile a nice list of (general) optimization functions for different algorithms, mostly so I don’t need to look them up one by one.  If an optimization method isn’t appropriate, I’ll summarize how you make a classification.  I will provide each function, as well as description, if appropriate:

Linear Regression

With linear regression, we aim to minimize the sum of squared error between our data and a linear equation (a line, our model). Specifically, we want to find the parameters, theta, that minimize this function (this is “ordinary least squares”:

We could do this with coordinate descent, however there is a closed form solution for this optimization:

The values of the optimal betas give us clues to how much of each feature, x, is used to determine the class.  The sign (+/-) of the beta value also hints at the relationship - a positive beta means that increasing the feature, x, increases our y, and a negative value means that they have an inverse relationship.  We can also assess if a beta is significant by calculating a p-value for how different it is from the null hypothesis (that the value == 0), i.e, think of a normal distribution of beta values, and if the value you obtained is in the tails (the .025 of values on the far left, or .025 of values to the far right) then it is significant, meaning that your beta value is unlikely to be due to chance.  Standard packages in R (lm) will automatically spit out these values for you.

Ridge Regression

When we place the L2 penalty on our betas (a), the result is ridge regression, and we want to find the values of a that minimize the following equation (subject to the penalty):

Obviously as our fudge parameter, lambda, goes to zero, we just get ordinary least squares.  Also remember that if we use the L1 penalty instead, (the absolute value of the summed parameters) we get lasso, and if we are totally undecided about which one to use, we can use elastic net and move our parameter alpha between 0 (ridge regression) and 1( lasso).  Broadly, I think of lasso, ridge regression, and elastic net as regularization strategies that can be used with standard regression.

Locally Weighted Linear Regression

When we have data with a non-linear distribution, we can take a non-parametric approach and use locally weighted linear regression:

The equation is the same, except now we are multiplying by a vector of weights, w, that place high weight on the points closest to our training example.  This means that we are looking at local neighborhoods of our data, and building a model for each local neighborhood.  This is obviously computationally intensive, and does not give us a nice “final equation” for our model.  We have to keep the data around (akin to knn) to make a classification.

The weight function takes into account a tuning parameter (the “bandwidth”) that specifies how big the step should be between neighborhoods.  If we choose to build a model at every data point (a small bandwidth), you can imagine that we would estimate our function very well, however there is probably some overfitting going on.  It would be better to increase the bandwidth to get an abstraction of the data, but not make it so big that we lose the general shape of our non-linear distribution (e.g., you can imagine if you choose the “neighborhood” to be the entire dataset, you are essentially just fitting a linear model to your data).

Naive Bayes

Naive Bayes assumes independence of features, and allows us to figure out the probability of a particular class (y) given the features by looking at the probability of the features given the class:

We use our data to calculate the priors (the probability of a class being == 1, and the overall p(x), calculate this probability for each of our classes (0 and 1 in a simple example), and then just assign the class with the higher probability.

SVM with regularization

We want to build our model by finding the non-zero parameters that form our supporting vectors.  We solve for our parameters by maximizing the following equation:

The above is the SVM optimization with regularization, meaning that we are additionally imposing an L1 penalty on our parameters (C is akin to lambda), and it simplifies to be exactly the same as without the regularization, but the parameters also have to be less than or equal to some C.  We can solve for the optimal parameters by way of the SMO Algorithm.

Logistic Regression

Logistic regression models the probability that a class (our Y) belongs to one of two categories.  This is done by using the sigmoid function, which increases nicely between 0 and 1, giving us a nice probabilistic value.  This is our hypothesis (h(x)), and it’s also called the “logistic function.”  This is the log likelihood equation that we want to maximize, and we could do this similarly to linear regression with gradient descent (e.g., take the derivative of the function below with respect to the parameters, plug into the update rule, cycle through your training examples and update each one until convergence):

Gaussian Discriminant Analysis (GDA,LDA,QDA)

Independent Component Analysis (ICA)

With ICA we model our observed data as a matrix of weights multiplied by a matrix of “true” signals, which implies that the observed data is some linear combination of these original signals.   We assume independence of our signals, and so we model them with some function that “gets at” independence, e.g., kurtosis, entropy, or neg-entropy, and then we maximize this value.  We could also model the distribution of each component with sigmoid (increasing between 0 and 1), multiply to get the likelihood function, then take the log to get the log likelihood, and then take the derivative to get a stochastic gradient descent rule, and update the matrix of weights until convergence.  The equation for the log of the likelihood is as follows:

And then the update rule for stochastic gradient descent would be:

Principal Component Analysis

With PCA we want to decompose our data based on maximizing the variance of our projections.  We model this by summing the distance from the origin to each point, and then dividing by the number of points (m) to get an average.  We then factor our distance calculation (L2 norm in the first equation), and we see that this simplifies to the principal eigenvector of the data multiplied by the covariance matrix (in parentheses, third term).  This means that PCA comes down to doing an eigenvalue decomposition (factorization) of the data.

and then once we solve for the eigenvalues (u), we project our data back onto them to get the new representation:

Archetypal Analysis

We start with the same model as ICA, except we don’t assume independence of signals, so we just model our data (X) as a linear combination (W) of some set of archetypes (H), so X = WH.  We also model the archetypes (H) as some linear combination (B) of the original data (X), so H = BX.  We then would obviously want X - WH to be equal to zero, and also by substituting in BX for H we get the equations that we want to minimize:

We would minimize this function in an alternating fashion.

Non negative matrix factorization

Again, is the same basic model as ICA and Archetypal (above), however we model each resulting component with poisson, and then we can maximize the likelihood or minimize the the log of the likelihood:

Kernel Methods

Kernel methods, most commonly described in relation to support vector machines, allow us to transform our data into a higher dimensional space to assist with the goal of the learning algorithm.  Specifically for SVMs, we are looking to define the support vectors based on maximizing the geometric margin, or the distance between the dividing line and the support vectors.  What this come down to is minimizing a set of weights subject to constraints that some are positive, and some negative, and the ones that turn out to be greater than zero indicates a functional margin == 1, and they form the support vectors.  Abstractly, we are finding the line to draw through our data (or some transformation of it, thanks to the kernel) so we can draw a line through the two classes.

Kernel methods aren’t just useful for SVMs.  We can also use them with linear discriminant analysis, principal component analysis, ridge regression, and other types of clustering.  For this post, I’d like to outline some popular choices of kernels.

How do I know if a function can be a Kernel?

If you have some function, it must satisfy two conditions to be a kernel:

1. The kernel matrix (an mxm matrix for which each value has your Kernek, K(xi,xj) defined at each slot ij) must be symmetric.
2. It must also be positive semi-definite (K >= 0)

These conditions were figured out by Mercer, and detailed in Mercer’s theorem.

Types of Kernels

It’s not clear to me what the best way to choose a kernel is.  From reading, it seems that many people choose the radial basis kernel, and if left on my own, I would probably just try them all, and choose the one with the lowest cross validated error.  Graph kernels calculate cross products for two graphs.  String kernels are used with strings.  Popular choices for imaging are radial basis and Fisher kernels, but there are many other types, and you will have to read about the best types for your particular application.  Here are a few additional notes:

Choosing a Kernel

In being like a dot product, a Kernel is essentially a similarity function.  For example, think of  euclidean distance, for which you calculate by taking the square route of the dot product.  A small value means that some two vectors are close together, and a large value means that they are not.  So, if a Kernel is like a dot product, it should result in small values when applied to similar objects, and large values when applied to different objects.

RBF Kernel (Gaussian)

The radial basis kernel is a good default choice when you’ve established that you have some non-linear model.  I also read that it’s a good choice for image classification because it selects solutions that are smooth.

Linear kernels

I read that they typically are much faster than radial based ones.

Polynomial kernel

A better choice for text classification problems, commonly with the exponent = 2.

The Gap Statistic

The gap statistic is a method for approximating the “correct” number of clusters, k, for an unsupervised clustering. We do this by assessing a metric of error (the within cluster sum of squares) with regard to our choice of k. We tend to see that error decreases steadily as our K increases:

However, we reach a point where the error stops decreasing (the elbow in the picture above), and this is where we want to set our value of k as the “correct” number. While we could look at a plot and estimate the elbow, better is a formalized procedure to do this. This is the gap method proposed by the awesome statistics folk at Stanford, and it can be applied to any clustering algorithm with a suitable metric to represent the error.

The idea behind the Gap Statistic

We have this graph that compares the error rate (K-Means WCSS, for example) to the value of k. We can only get a sense of “how good” each error/k value pair is if we are able to compare to the expected error for the same k under a null reference distribution. In other words, if there was absolutely no signal in data with similar overall distribution and we clustered it with k clusters, what would be the expected error? We want to find the value of k for which the ‘gap’ between the expected error under a null distribution and our clustering is the largest. If the data has real, meaningful clusters, we would expect to see this error rate decrease more rapidly than its expected rate. This means that we want to maximize the following equation:

The first term is the expected error under a null distribution, and the second is our particular clustering.  We take the log of both (I think) to standardize the comparison, allowing us to make comparisons between different data and clusterings.

How do I choose a reference distribution?

The paper behind this method suggests two strategies:

1. Generate the distribution uniformly over all observed values for each feature.
2. Use the same strategy as above, but applied to the singular value decomposition (svd) of your data, so your uniform distribution is generated from a source that gets at the general structure of your data.  You would have to first generate the distribution and then back transform to get the reference data.

and then nicely lays out the algorithm for the entire procedure:

1. Cluster your data over some range of k = 1 … K
2. Generate B reference data sets using a or b above.
3. Cluster your references
4. Compute the gap statistic as follows:

This is the same equation that we saw before, except that we are taking an average over our b reference distributions.  We then would want to calculate the average expected error for just the reference distributions, this is the “mean” (muuuu!) that of course is a metric to define the distribution. Let’s call this l:

And then of course we can plug our mean (muuuuu!) into the equation to calculate our standard deviation (“gets at” the spread of our reference data):

 :

of course, now we need to remember that since this is simulated data, there is likely error.  We need to account for this error.  I don’t quite understand the rationale behind this equation, but if you imagine you have some number of B reference distributions between 1 and infinity, we are essentially multiplying our standard deviation by a value between 1 and sqrt(2):

thus making the variance just a little bit larger, because we probably underestimated it with our sampling?  Let’s now choose our number of clusters, k, based on the Gap(k+1) having as much distance as possible from the gap at the previous value of k:

The equation above is looking at two values of k, specifically “k” and “k+1.”  We want to choose the value of k that maximizes our gap, adjusted for the expected variance (sk+1 from our null reference).  The reason that we are assessing subsequent pairs, k and k+1, is because we don’t want to blindly look across all values of K, we want to choose the smallest one.  I don’t have rationale behind this idea, but I’d say that for two pairs of k and k+1 for which the Gap statistic is equivalent, the pair of smaller values is probably more correct.  E.g., it seems more reasonable to say that we have 5 “correct” clusters than 25.  I’m not sure about this, however.   Here is an example, also from the paper, applied to K-Means clustering:

The plot on the left shows the log of the expected error (E) from the reference distribution, compared to the observed data (O).  We can see that the difference between these two values (sort of) looks greatest at k=2.  The plot on the right shows the calculated Gap Statistic for this data, and we can see that it is indeed maximized when k=2.  The plots above are a good demonstration of what we see when there is real, meaningful clustering in our data.  What about when there isn’t? We might see something like this:

The plot on the right shows that the expected error is actually less than the observed error, and the corresponding Gap statistic on the right has all negative values.  This tells us that there is no value of K for which there is a good clustering.