vsoch

Segmentation of MRI with Bayesian Methods

Let’s say that I am a proponent of the idea that I can segment the brain into meaningful regions (e.g., caudate, amygdala, hippocampus…), which some may think is akin to cutting up the United States into said states.  This could be useful to assess differences in morphometry (the study of shape) between two populations.  This task is more challenging than the task of segmenting based on tissue type (white, gray, csf), because most of these anatomical regions that we are interested in are the same tissue type, namely gray matter.  How could I do this?

Manual Segmentation: I could use my favorite software package, click through the slices, and define regions manually.  I don’t really want to do that, because it would take forever.

Image Intensity Segmentation: This obviously doesn’t work, because most of these regions are going to have huge overlap in image intensity.  The image below (from Fischl et. al 2002) shows this overlap nicely:

…and in fact, this paper lays out the basic methods that underlie the subcortical segmentation procedures for the software package freesurfer.  I’ll be upfront with you and tell you that I’m writing this post in the first place to better understand this subcortical segmentation, because I don’t like using black boxes.  Let’s walk through these methods!  The strength comes by way of incorporating spatial information.

Incorporate Spatial Information:?  Yes!  A good way to go about this must include some kind of spatial information about where each subcortical structure “should” be.  This “should” hints at some kind of probabilistic approach.  In fact, we need a probabilistic atlas.  This is where some people might get uncomfortable, because any kind of atlas is made by averaging over many brains, and this average may not be representative of the group that the atlas is used with.  This approach is strong, however, because we can model the probability of a particular structure being in a certain place independently of the intensity.  But we don’t want to completely throw intensity away, because if you look at the plot above, you will see that some subcortical structures do have significant differences in intensity.  It’s only when we shove everything into a tissue class (e.g., gray matter) that we widen the distribution and lose this distinction.

Incorporate Neighboring Voxels?:  This is another way of incorporating spatial information, and it’s based on the idea that we generally find structures in the same spots relative to one another.  Instead of just modeling the intensity and prior probabilities of any voxel in the brain belonging to a particular structure, we are going to assess if a voxel is likely to belong to a structure given its neighboring voxels.  For example, if I’ve labeled a voxel as being in the prefrontal cortex, what is the probability that a neighboring voxel is… part of the cerebellum?  Obviously zero! 😛  But you get the idea.  To do this we will use Markov Random Fields (MRF), which will let us model the probability of a label given the neighboring labels.

Our Segmentation Approach

1. Calculate the means and covariance matrices of each region of a set of anatomical structures using linear methods to register a brain with an average template
2. Calculate prior probabilities of each anatomical structure with a frequency histogram, and with this we will calculate the probability that any particular label occurs in a certain location
3. Incorporate this prior probability of a particular spatial arrangement of labels into segmentation.

Model the Segmentation in a Bayesian Framework

We start by modeling the probability of the segmentation, W, given the observed image, I:

The P(W) is the prior information about the segmentation.  Both this P(W) and the probability of the image given the segmentation, for this application, can be modeled in an atlas space, meaning that the function varies depending on where we are in the brain. For example, the probability that a segmentation has a particular region, r, that is equal to some class, c, is represented by:

P(W(r) = c)

What can we say about this?  Since we have many anatomical labels, many of them small,  we can say that for a set region, r (think one voxel in the brain), we can look at all of its potential class labels, c, and most of these are going to have a probability of zero.    The number of possible classes for each location is pretty small (the average is actually around 3, and it rarely is > 4).  This reduces our problem of needing to classify all the voxels in the brain into some 40+ subcortical classes into needing to classify each voxel into maybe 3-4 labels. See, including spatial information is kind of a good idea!  Now we need a function that can take a particular spot in the subject’s native space, and find the corresponding spot in the atlas (this is the basic definition of an atlas, period).

Add in a Function to Map Native Brain Space –> Atlas

In order to use our probabilistic atlases with some person’s unique brain, we need to be able to map each voxel in the native brain to the “correct” one in the atlas.  This is our “normalization” step, which lets us relate coordinates across different people.  Let’s call this function f(r), and let’s place it in the context of our atlas function:

The equation now says “the probability of a particular segmentation and normalization of a person’s brain given the imaging data can be expressed as a function of:

• P(I

  W,f):  This is the relationship between the predicted image intensities and the class label.  Unfortunately, this term does depend on specifics of the scanner where the image is acquired, and we reduce this independence by instead modeling this term in terms of the relationship between the image intensities (n) and acquisition parameters (b):

The tissue parameters, b, can be estimated with MR relaxometry techniques, meaning that instead of modeling the conditional densities for each class in terms of the actual image intensities, we model them in terms of the T1 relaxation times for each class.  The second term to the right of the equals sign, the probability of the tissue parameters, can be estimated using manually labeled subjects (more on this in the next section).

• P(W	f): This is the probability of an anatomical class given the spatial location

• P(f): This constrains our atlas functions based on the normalization

How do we make the probabilistic brain atlases?

I keep mentioning these atlases that have prior information about classes for any particular anatomical location.  For most neuroscientists that download software, click on the GUI buttons, and plug and chug their data through an analysis, these probabilistic maps come with the software.  The harsh reality is that at some point, in order to have these atlases, someone had to make them.  There are two possible ways someone might go about this:

• Use an individual as a template brain, and register many other people to this template brain.  In this context, each voxel represents a unique anatomical region.  The problems with this approach, of course, are that we are hugely biased based on whomever we have chosen as the initial template.
• Average across many brains to create a fuzzy picture of the average intensity for each voxel.  This means that we only retain common brain structure.  The problem with this approach is obvious - we remove interesting variation among people.

Model the intensity distribution for each class, each voxel, as Gaussian:

To address the problematic approaches above, we strive for a method that can preserve information about each class label for each voxel.  We first need to do some dirty work, namely, taking a large set of brains and manually segmenting them into our different classes.  We can then, for a particular voxel, estimate the prior probability for each class, c:

Now we need to model the intensity distribution for each voxel, r.  If you’ve ever been bored and randomly modeled the intensities of a particular dataset, the distributions tend to look Gaussian, so we do that.  What do we need to define a Gaussian?  A mean and standard deviation, of course.  The equation below is how we get the mean (muuuu!) for a given location (r) defined over a set of M images:

The term Ii (I think) is like an indicator variable - in each image, M, we add 1 to the count if the label c occurs at the location r.  Then we divide by M to get an average, our mean.

Then we can get the covariance matrix by plugging in the same terms that we used above to the standard calculation of covariance:

The above two steps give us the parameters to define a Gaussian intensity distribution for each voxel location, r, for some class c.  So in the context of many classes, we have one of these guys for every single class, for every single voxel location.  Whoa.  This improves upon our “average brain” approach because we don’t need to average intensities across classes.

 Calculate Pairwise “Neighbor” Probabilities

Remember how I mentioned that we want to be able to take some voxel location, r, and model the probability of a certain class given the neighboring classes?  We can also do this using our manually labeled images.  The equation below says that we can estimate the probability of a certain voxel, r, being class c given the classes of the neighboring voxels:

Each of the ri terms represents one of the neighbor locations of voxel r, and I think the little m just represents our M images.  For the above equation, for each pair of classes, for each voxel, r, we count the number of times that the second class is a neighbor when the first class is defined at the voxel, and divide by the number of times the first class is defined at the voxel.  We have to store these probabilities for each pair of voxels, for each class.  You may be asking, “Wouldn’t this make my computer explode?” and the answer is actually no, because a lot of these probabilities will turn out to be zero, and there are very efficient ways in computer science for storing zeros.

Defining the Function to Normalize Brains, Least Sum of Squared Intensity Differences?

The function mentioned above, f(r), is going to help us to get a rough alignment for people’s brains, and this is where we throw in our favorite registration algorithm for our images, M, to some standard template like the Talaraich atlas or MNI template, both created based on the approach of defining a “common brain.”  The standard method is to use intensity information (because the images are from the same modality), and align locations in the brain with similar intensities by finding the linear transformation, L, that minimizes the least sum of squared error between an individual’s brain (I) and the template brain (T).  This will result in a registration that will likely have different tissues aligned on top of each other for different subjects.

We can actually do better, although we are faced with quite a problem. We want to maximize the probability of the segmentation given an observed image, however neither the alignment function or the segmentation are known.  We would need to maximize the joint probability of these two things, again, this equation:

and the result would be the Maximum a Posteriori (MAP) estimate.  If you read about common methods to go about this (e.g., Gaussian pyramids), it comes down to again averaging across smoothed images, which we don’t want to do.  So, what should we do?

Defining f(r) with LSS Intensity Differences with a meaningful subset of voxels!

For hundreds of thousands (or even millions) of parameters, finding an alignment function, L, to minimize the sum of squared error for intensity differences is REALLY HARD.  Could there be a way to drastically minimize the number of paramters that we need to estimate?  Yes!  Let’s think back to the equation that calculates the probability of a class for a particular equation, r:

Although people’s brains don’t line up perfectly, there are actually a good number of voxels (think of voxels toward the center of defined regions) for which this probability approaches 1.  For these voxels, the segmentation is done - we know the class label.  So we can actually come up with a subset of voxels for which our segmentation is “known.”  We can now find the alignment transformation, L, that maximizes the likelihood of this sample.

How do we choose the subset of voxels?

The voxels that we choose for this subset must fit the following criteria:

• Remember that we are working within the scope of one class label, c.  Thus, we choose voxels for which the probability of c is greater for that label than any other label.
• We also choose voxels for which the probability of our class is greater for that particular location than any other location.

This will define a subset of a few thousand voxels, down from hundreds of thousands.  We can now find our affine transform, L, that maximizes the probability of the transform given the segmentation and images:

Segmentation (Finally) with Bayesian Methods

As a reminder, the guts of this method are doing a segmentation based on priors (probabilities) about a particular voxel being a class, c, based on 1) spatial information and 2) neighboring voxels:

Solving for P(I|W,L)

over R voxels in the entire image.  Since we went through and calculated the means and covariance matrices for every class and voxel earlier, we can calculate this product by plugging in these values to a Gaussian density function, specifically:

Solving for P(W|L)

The Markov assumption says that we can calculate the prior probability of a label at a given voxel, r, based on the voxels in its neighborhood, in the set {r}:

I’m not great in my knowledge of statistical distributions, however there is a particular one called a “Gibbs distribution” that embodies this Markov assumption, so we can equivalently model the P(W) using this distribution:

I won’t go into the details, but Z is a normalizing constant, and U(W) is an energy function (see the paper linked at the beginning of the post for a more satisfactory explanation).  This allows us to write the probability of the segmentation as the product of the probability of the class at each location, given the neighborhood:

This would be computationally impossible to implement, so instead we model the dependence of a label on its neighbors based on the probability of the label given each of the neighbors:

Now we can plug in the above into the long second term in our equation for P(W) (two equations up) to get a final equation for the prior probability of a segmentation:

• P(W(r)): tells us the probability of a particular structure being in a location, r.
• The term in the second product gives us the probability of the structure given the neighbors labels.  Now we have our P(W), and we can use the iterated condition modes (ICM) algorithm to find the label, c, that maximizes the conditional probability.  This procedure is done iteratively until no voxels are changed (and this is covergence).

There are some pre and post-processing steps detailed in the paper, however the above summarizes the general approach.  We would now have a segmentation of an individual’s brain for each voxel, r, into different classes, c, using probabilistic atlases that incorporate spatial and neighborhood information.

On to Freesurfer!

We can now venture into subcortical segmentation in freesurfer with a little more understanding of what is going on under the GUI, and come up with beautiful delineations, as shown below, demonstrating the method in action.  And (hopefully) we can build on this understanding to extend the tools for our particular goals.

Dimensionality Estimation of ICA with Bayesian Analysis

Across methods of matrix decomposition (ICA, Archetypal Analysis, NNMF), we run into the problem of needing to know how many signals to decompose our data to.  This is called model order selection.  If we choose a number that is too small (underestimation) then we lose information and our decomposition is sub-optimal.  If we choose a number that is too big (overestimation), we create a bunch of spurious components and overfit the data.  As a reminder, these  methods assume that our data (X) is some linear combination of some N “true” signals (S), meaning that:

X = WS

where W is a matrix of weights that we apply to our matrix of signals to mix things up a bit.  In the case of ICA we assume that these signals are independent, and for the other two methods we do not assume independence, but we start with positive data so our matrix of weights is also positive.

How do we do ICA in the presence of Gaussian noise?

Since ICA is either maximizing the independence of the signals by way of kurtosis maximization / minimization, entropy maximization (Infomax agorithm), or neg-entropy maximization (FastICA), shouldn’t it make sense that if we have noise (which has a Gaussian distribution), this messes up the method?  Well, we could allow for one signal with a Gaussian distribution, but as we remember that any Gaussian can be expressed as the combination of other Gaussians, we can’t have more than one, otherwise we can’t unmix the signals.  So, in the case of multiple Gaussians thrown into the mix, we need methods that deal with this, or methods that can accurately estimate the amount of Gaussian noise.  With the standard Infomax approach applied to neuroimaging data, we don’t model the noise.  We in fact assume that the data can be completely characterized by the mixing matrix and the estimated sources.  What this means in fMRI is that we tend to overfit our model to noisy observations.  This is when the famous Beckmann and Smith decided to create a probabilistic model that can control the distinction between what can be attributed to noise, and what can be attributed to real effects.

An ICA Method that will estimate order

This model assumes that the data is confounded by noise, and is going to help us generate our probabilistic model.  This model takes three steps to estimate sources:

1. We first estimate a signal and a noise subspace.  Specifically, we find the signal space with probabilistic Principal Component Analysis (PPCA), and the noise subspace is orthogonal to this signal space.  In this step we will estimate our number of components.
2. We then estimate our sources (with FastICA)
3. We then assess if the estimated sources are statistically significant

(I will discuss PICA and PPCA in detail in another post) - for now let’s start with this as our framework, and know that by using the probabilistic ICA model (PICA) we a specified order, q, we will get a unique solution.

Normalize the data

As a preprocessing step, although this may make some squirmy, we normalize the original data timecourses (meaning each voxel over time) to have zero mean and unit variance (this means subtracting the mean and dividing by the standard deviation).  This assumes that all voxel’s time courses are generated from the same noise processes.  We do this because, in this space, any component that isn’t noise will need to jump out and say “Hello, look at me! I’m non-Gaussian!”

Model order selection

We figure out the dimensionality of our decomposition based on the rank of the covariance matrix.  Remember that covariance is a measure for how much two variables change together.  If change in one variable changes the other by the equivalent amount, covariance = 1.  If there is an equivalent change in the other direction, covariance is -1.  If one variable doesn’t influence the other at all, covariance is 0.  So if our observations are in a vector, xi, then we want to create a matrix that, in any coordinate ij, specifies the covariance between the point xi and the point xj (and remember in this case, a “point” is referring to a voxel location).  If we have absolutely no noise, we know that the quantity q (the correct dimensionality) is the rank of the covariance of the observations:

Our observations, x, have length m (the number of timepoints), and this results in a mixing matrix of size mxm, so the rank is m, so our dimensionality, q, is q = m:

The equation above says that the rank of x is the rank of the dot product of the vector xi, which is the same as our mixing matrix A.  However, in the presence of noise, this means that the eigenvalues of the covariance matrix are raised by adding some sigma squared:

This is really thick reading, but I will do my best to explain how I think this works.  The covariance matrix, Rx, is a square matrix so it can be expressed in terms of its eigenvectors and eigenvalues.  If you look at the relationship between eigenvalues/vectors and the original square matrix, multiplying the eigenvectors by the matrix of eigenvalues (down the diagonal, like a trace) is equivalent to multiplying the original matrix by the eigenvectors.  I think this abstractly implies that the eigenvalues can be used as a representation of the original matrix, Rx.  In this case, if we were to find identical eigenvalues, arguably, this is repeated information.  And so finding the correct dimensionality, or the rank, of the matrix Rx boils down to finding the number of identical eigenvalues.  However, in the case of noisy data (like fMRI) this becomes problematic because we can’t look for “exact” equality, we have to assess equality within some threshold.  We need a statistical test for the equality of these values beyond some threshold.

Using prediction likelihood as a test for equality

We could decide to choose our threshold for assessing if two eigenvalues are “close enough” to be equal –> choosing the rank of the covariance matrix –> choosing the correct ICA dimension based on maximizing the likelihood of our original data, X.  Would that work?  It would mean going through a range of thresholds, applying them to our eigenvalue and vector matrices to reproduce the “new” (reduced) covariance matrix, and then seeing what percentage of variance our model accounts for out of the total variance of the data.  I’m guessing that since the covariance matrix is simply a generalization of variance to multiple dimensions, a simple method would be to assess [total variance of thresholded model]/[total variance of original model] and try to maximize that.  But wait a minute, doesn’t that mean that we could just keep decreasing the threshold (adding more eigenvalues and thus increasing the rank and proposed dimension) and we would obviously be better approximating the original data and probably get up to accounting for 99.9% of the original variance with our model?  I think so.  That doesn’t help us to estimate the “true” dimension of the data.  What else has been proposed?

Using the “scree plot” to determine meaningful eigenvalues

A scree plot shows the ordered eigenvalues on the Y axis, and components on the X axis. It was suggested that finding a “knee” in this plot is akin would be a good way to estimate the correct dimensionlity, because some true N eigenvalues are meaningful about the data, and then when the values drop off, beyond that “knee” are junky ones.  If you look at the first page of FSL’s MELODIC tool (that performs ICA with this automatic estimation, shown below), you will see this scree plot:

The eigenvalues (purple line) decrease as we move from left to right, and with this we like to see the percentage variance that our choice of dimensionality accounts for (the green line).  Obviously if we include all the components (meaning that we don’t filter out any eigenvalues and the covariance matrix is assessed at its original rank) we account for 100% of the variance.  But as stated previously, accounting for 100% variance in the model is not akin to finding the correct dimension of the data!  In the case of the chart above, you can see why using the “knee” of the scree plot to estimate dimensionality is considered “fudging.”  Is it around 4ish? 6ish?  Closer to 12?  Clearly this is not reliable or robust.  Wait, what is that funky red line, the “dim. estimate” referring to?  Maybe a better way to estimate the dimensionality!

Random matrix theory to estimate dimensionality?

Before I discuss the approach that FSL’s software uses, I want to review how random matrix theory can help us.  Actually, I don’t claim to have a solid definition for what random matrix theory is, but it looks like it means filling up a matrix with random numbers from some specified distribution.  In this case, it looks like if we had completely Gaussian noise, our covariance matrix would follow a particular distribution called a Wishart Distribution.  We can then look at the eigenvalues for this “base case” covariance matrix that is all noise, and compare to our covariance matrix, which has some true signal + noise.   The eigenvalues that are in our model but not encompassed in the eigenspectrum of an equivalently sized random Gaussian matrix, then, are the meaningful ones reflective of of the true signal.

Order Selection in a Bayesian Framework

This is the method that FSL actually uses (I believe), and it was proposed by Minka in 2000 in this paper.  Minka presented a Laplace approximation to the posterior distribution of the model evidence (e.g., how many eigenvalues to include).  Again, we are going to work with the eigenspectrum of the covariance matrix (Rx) to figur this out.  Let’s walk through this.  Since this is a bayesian approach, we want to maximize the probability of our data, X, given our choice of dimensionality, q:

This means that we will need to define some uniform prior over all possible eigenvector matrices.

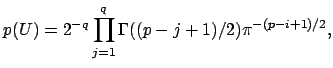
I’m not going to pretend to be able to explain this equation, I need a few hours to walk through the paper that I linked above.  Intuitively, we can see that we are summing over possible square eigenvector matrices from size j=1 to the full size, q.  This equation is described as “the recipricol of the manifold” as defined by James in 1954.  Look at page 5 here, or the James paper here.  Having only taken introductory stats courses in my life, I’m going to take the equation above as is, it is our prior to represent the summed probability of all our eigenvector matrices.  We then can model the probability of our data, X, given a value of q as follows:

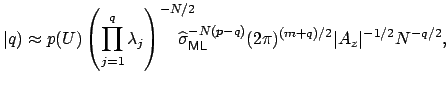
where

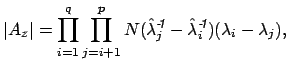
These equations look like death!  For full details about the variables, see here.  Basically, we find the correct dimensionality by choosing q that maximizes this equation.  I’m guessing that the red line in the plot above is reflective of this changing probability, but I’m not sure.

A final note about the big picture

I’m someone that likes details, and so I am prone to get lost in said details and completely forget about the big picture.  It’s a fulfilling and frustrating thing.  On the one hand, it feels great to dig into something and truly understand it.  On the other hand, being human means that there are only so many hours per day to distribute between work and study, and so those hours must be allocated to maximize efficiency, or doing the things that I need to do in order to be a successful researcher and student.  For any topic that we learn about, you can imagine a plot of time spent on the x axis, and payoff on the y axis.  When we first start to learn about some new thing, there is huge payoff, but then the payoff drops with each additional unit of time until we reach some point when it doesn’t make sense to keep learning.  And so for a detail oriented person, this is a very frustrating point.  It means that at some point many things turn into a black box, and unless I want to unwisely allocate my time, I have to settle and take some things at face value.  Time would be much better spent learning other things that present with the same much higher initial payoff.

On the other hand, learning about algorithms is a lot like being a runner, and taking runs and bike rides to learn about a new city.  The new city is a method, and the intricate corners and streets represent the depth that I understand said method.  On my first outing, I choose a relatively safe route that sticks to main roads, and gives me the general gist of a city.  Along the way I see many interesting places off to the side that, perhaps at some later date, I can come back to explore.  On subsequent runs I go back to these places and learn more about the city.  However, no matter how many times that I can go out, I have to accept that it is not feasible to inspect every atom of every corner of every building.  Black box.

Mutual Information for Image Registration

Mutual information is an important concept for medical imaging, because it is so prominently used in image registration.  Let’s set up a typical registration problem.  Here we have two pictures of something that you see everyday, a dancing pickle!

I’ve done two things in creating these images.  First I’ve applied a simple translation to our pickle, meaning that I’ve moved him down and right (a linear transformation), and I haven’t warped or stretched him in any way (a non-linear transformation).  I’ve also changed his intensity values so that a bright pixel in one image does not correspond to a bright pixel in another image.  Our goal, is to register these two images. Abstractly, registration is pretty simple. We need to find some function that measures the difference between two images, and then minimize it.

Registration with minimizing the sum of squared distances

The most basic approach would be to say “ok, I want to find the alignment that minimizes the sum of squared distances,” because when pickle one is lined up with pickle two, the pixels should be the same, and so our error is small, right?  Wrong!  This is not a good approach, because a high intensity in one image does not mean the same thing as a high intensity in the other.  An example of this from medical imaging is with T1 and T2 images.  A T1 image of a brain has shows cerebral spinal fluid as black, while a T2 image shows it as bright white.  If we use an algorithm that finds a registration based on minimizing the summed squared distance between pixels, it wouldn’t work.  I’ll try it anyway to prove it to you:

% Mutual Information
% This shows why mutual information is important for registration, more-so
% than another metric like the least sum of squares.

% First, let's read in two pickle images that we want to register
pickle1 = imread('pickle1.png');
pickle2 = imread('pickle2.png');

% Let's look at our lovely pickles, pre registration
figure(1); subplot(1,2,1); imshow(pickle1); title('Pre-registration')
subplot(1,2,2); imshow(pickle2);

% Matlab has a nice function, imregister, that we can configure to do the heavy lifting
template = pickle1; % fixed image
input = pickle2; % We will register pickle2 to pickle1
transformType = 'affine'; % Move it anyhow you please, Matlab.

% Matlab has a function to help us specify how we will optimize the
% registration. We actually are going to tell it to do 'monomodal' because
% this should give us the least sum of squared distances...
[optimizer, metric] = imregconfig('monomodal');

% Now let's look at what "metric" is:
metric =

registration.metric.MeanSquares

% Now let's look at the documentation in the script itself:
% A MeanSquares object describes a mean square error metric configuration
% that can be passed to the function imregister to solve image
% registration problems. The metric is an element-wise difference between
% two input images. The ideal value of the metric is zero.

% This is what we want! Let's do the registration:
moving_reg = imregister(input,template,transformType,optimizer,metric);

% And take a look at our output, compared to the image that we wanted to
% register to:
figure(2); subplot(1,2,1); imshow(template); title('Registration by Min. Mean Squared Error')
subplot(1,2,2); imshow(moving_reg);

Where did my pickle go??  

Registration by Maximizing Mutual Information

We are going to make this work by not trying to minimize the total sum of squared error between pixel intensities, but rather by maximizing mutual information, or the extent to which knowing one image intensity tells us the other image intensity. This makes sense because in our pickle pictures, all of the black background pixels in the first correspond to white background pixels in the second. This mapping of the black background to the white background represents a consistent relationship across the image. If we know a pixel is black in one image, then we also know that the same pixel is white in the other.

In terms of probability, what we are talking about is the degree of dependence between our two images. Let’s call pickle one variable “A” and pickle two variable “B.”

If A and B are completely independent, then the probability of A and B (the joint probability, P(AB)) is going to be the same thing as multiplying their individual probabilities P(A)*P(B). We learned that in our introductory statistics class.

If A and B are completely dependent, then when we know A, we also know B, and so the joint probability, P(AB), is equal to the separate probabilities, P(AB) = P(A) = P(B).

If they are somewhere between dependent and independent, we fall somewhere between there, and perhaps knowing A can allow us to make a good guess about B, even if we aren’t perfect.

So perfect (high) mutual information means that the pixels in the image are highly dependent on one another, or there is some consistent relationship between the pixels so that we can very accurately predict one from the other. Since we have the raw images we know the individual probability distributions P(A) and P(B), and so we can measure how far away P(AB) is from P(A)P(B) to assess this level of dependence. If the distance between P(AB) and P(A)P(B) is very large, then we can infer that A and B are somewhat dependent. More on this computation later - let’s take a look at mutual information in action.

% Now let's select "multimodal" and retry the registration. This will use
% mutual information.
[optimizer, metric] = imregconfig('multimodal');

MattesMutualInformation Mutual information metric configuration object

A MutualInformation object describes a mutual information metric
configuration that can be passed to the function imregister to solve
image registration problems.

% Now the metric is mutual information! Matlab, you are so smart!
moving_reg = imregister(input,template,transformType,optimizer,metric);

% Let's take one last look...
figure(3); subplot(1,2,1); imshow(template); title('Registration by Max. Mutual Information')
subplot(1,2,2); imshow(moving_reg);

Hooray! Success! 

Mutual Information - the Math Behind It!

We’ve shown that mutual information is the way to go to register two images with different intensity values (i.e., different modalities).  Here is the actual equation to measure mutual information (this is the value that we would iteratively try to maximize)

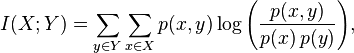
This is for discrete distributions, and if we had continuous distributions the summations would turn to integrals, and we would add dxdy to the end.  Given that we are summing probabilities, this value always has to be positive.  Can you see what happens when our variables are completely independent, when p(x)*p(y) = p(x,y)?  We take a log of 1, and since that is 0, our mutual information  is also 0.  This tells us that knowing A says nothing about B.

Kullback-Leibler Divergence - Another measure for comparison

The above reads, “the KL divergence between some real distribution, P, and our model of it, Q, is the expectation of the logarithmic difference (remember that a fraction in a log can be rewritten as log(top) - log(bottom)) between the probabilities P and Q, where the expectation is taken using the probabilities P.”   Again, when our model (Q) fits the reality well, (P) ad the two probabilities are equal, we take the ln(1) = 0, and so we would say that “zero information is lost when we use Q to model P.”

The above code is also available as a gist here.

Multidimensional Scaling (MDS)

Multidimensional scaling (MDS) is a way to reduce the dimensionality of data to visualize it.  We basically want to project our (likely highly dimensional) data into a lower dimensional space and preserve the distances between points.  The first time that I learned about MDS was by way of STATS 202 with John Taylor, although to be honest, I got through the class by watching old lectures by David Mease on youtube.  Thank goodness for youtube!

If we have some highly complex data that we project into some lower N dimensions, we will assign each point from our data a coordinate in this lower dimensional space, and the idea is that these N dimensional coordinates are ordered based on their ability to capture variance in the data.  Since we can only visualize things in 2D, this is why it is common to assess your MDS based on plotting the first and second dimension of the output.   It’s not that the remaining N-2 axis don’t capture meaningful information, however they capture progressively less information.

If you look at the output of an MDS algorithm, which will be points in 2D or 3D space, the distances represent similarity. So very close points = very similar, and points farther away from one another = less similar.  MDS can also be useful for assessing correlation matrices, since a correlation is just another metric of similarity between two things.

How does MDS Work?

Let’s implement very simple MDS so that we (and when I say we, I mean I!) know what is going on.  The input to the MDS algorithm is our proximity matrix.  There are  two kinds of classical MDS that we could use:

• Classical (metric) MDS is for data that has metric properties, like actual distances from a map or calculated from a vector
• Nonmetric MDS is for more ordinal data (such as human-provided similarity ratings) for which we can say a 1 is more similar than a 2, but there is no defined (metric) distance between the values of 1 and 2.

For this post, we will walk through the algorithm for classical MDS, with metric data of course!  I’m going to use one of Matlab’s random datasets that is called “cities” and is made up of different ratings for a large set of US cities.

% Multidimensional scaling (MDS) Example

% Load matlab cities data
load cities

% This data has cities in rows, and different categories for ratings in
% columns. We will implement MDS to assess city similarity based on
% ratings.

% Step 1: Set up our proximity matrix
% First let's create our similarity (proximity) matrix by calculating the
% euclidean distance between pairwise cities
proximities = zeros(size(ratings,1));

for i=1:size(ratings,1)
for j =1:size(ratings,1)
proximities(i,j) = pdist2(ratings(i,:),ratings(j,:),'euclidean');
end
end

% Step 2: Create our centering matrix
% Now we need to perform double centering. I'm going to define these
% matrices explicitly so it's clear

% This is an identity matrix of size n, where n is the size of our nxn
% proximity matrix that we just made
n = size(proximities,1);

identity = eye(n);

% This is an equally sized matrix of 1's
one = ones(n);

% Here is our centering matrix, commonly referred to as "J"
centering_matrix = identity - (1/n) * one;

J = centering_matrix;

% Step 3: Apply double centering, meaning we square our proximity matrix,
% and multiply it by J on each side with a -.5 coefficient
B = -.5*J*(proximities).*(proximities)*J;

% Step 4: Extract some M eigen values and vectors, where M is the dimension
% we are projecting down to:
M = 2; % so we can plot in 2D
[eigvec,eigval] = eig(B);

% We want to get the top M...
[eigval, order] = sort(max(eigval)','descend');
eigvec = eigvec(order,:);
eigvec = eigvec(:,1:M); % Note that eigenvectors are in columns
eigval = eigval(1:M);

% Plop them back into the diagonal of a matrix
A = zeros(2);
A(1:3:end) = eigval;

% If we multiply eigenvectors by eigenvalues, we get our new representation
% of the data, X:
X = eigvec*A;

% We can now look at our cities in 2D:
plot(X(:,1),X(:,2),'o')
title('Example of Classical MDS with M=2 for City Ratings');

% Grab just the state names
% NOTE: doesn't work perfectly for all, but it's good enough!
% ALSO NOTE: The labels were hard to see, so they are not
% included in the graphic below.

cities = cell(size(names,1),1);
for c=1:size(names,1)
cities{c} = deblank(names(c,regexp(names(c,:),', ')+2:end));
end

% Select a random subset of 20 labels
y = randsample(size(cities,1),20);

% Throw on some labels!
text(X(y,1), X(y,2), cities(y), 'VerticalAlignment','bottom', ...
'HorizontalAlignment','right')

Here are our cities, with MDS applied, closer dots  = more similar cities, as assessed by ratings pertaining to climate, housing, health, crime, transportation, education, arts. recreation, and economics.

This isn’t the greatest example, because showing the labels wouldn’t give you much insight into if the method works.  (Better would have been to use a dataset of actual distances then projected into 2d, oh well!) The end of the script does format and display labels, however the picture doesn’t show them, because they didn’t add much.  For more details (and a better example that uses simple cities distances) see here.

Remember that this is an incredibly simple form of MDS.  See page 589 of Elements of Statistical Learning for more.

Imputation of Missing Values

In a perfect world, my data is absolutely perfect, and I’ve collected every feature or metric for every person, to be fed cleanly into some model.  Now let’s recognize the obvious reality that having complete data is rarely the case.  We usually having missing values (NAs) in analysis, and so we must consider methods to deal with these missing values.  There are two possible approaches:

1. We can drop all observations for which we have missing data
2. We can impute them, or come up with a good estimation of what they are likely to be
3. We can use a method that allows for missing values

Data is gold, and so option 1 is not ideal, although I’ll note that technically you should not have a problem with removing data if the missing values are completely random.  A good example of this is some questionnaire that asks about income.  People that leave the question blank may have a good reason (e.g., a super high or low income that they are embarrassed about), in which case dropping those cases would hugely bias your analysis.   Option 3 depends on your specific data and type of method, so I won’t review it just yet.    Let’s assume that we don’t want to boldly eliminate entire observations, and talk about option 2, or methods for imputing missing values.  This is by no means a comprehensive summary - it is the beginning of my thinking about this issue, and I will add to it as I learn more.

Imputation of Missing Values

• Mean imputation: replaces missing values with the mean of the values that we do have.  The problem with this approach, of course, is that it leads to underestimation of the standard deviation.  For just a few missing values, however, it may not be so bad.
• Last value carrier forward: In this approach, if we are missing some clinical outcome, we fill it in with the last value recorded for a pre-treatment measure.  This is a conservative approach because we are assuming no change, and so it biases our data toward the view that “whatever protocol was implemented, there was no significant change.”  If there is signal in our data to suggest otherwise, and it is a strong signal, it would need to overpower this bias for us to conclude that the intervention caused a significant change in outcome.
• knn-imputation: In this approach, we use a similarity metric to find the most similar observation(s), and fill in the missing value with that/those observations.  If you take more than one observation (K>1) then you would take a summary statistic.
• Random Imputation: In this approach, we place all of the variables that aren’t missing into a bucket, and we randomly sample from that bucket to fill in missing values.  This would get rid of the NaNs, however it does not take anything specific about the observations into account.  We are just filling the missing values in with a likely number from the distribution.
• Regression Based Imputation: In this approach, we again take the cases for which we have observed data, and we fit a regression to these cases, with the outcome variable, Y, being one of the missing variables that we want to predict.  We can then plug our data with missing values into the model (and fill in perhaps a mean value for features, X, that we are missing) to come up with  a prediction for Y.  While this again is making assumptions by filling in mean values for some of the variables X, minimally we are predicting our Y based on some knowledge about the observations, the X’s that we do know.  You could also select variables, X, for which you know that you have complete data.  With this in mind, if you have a large enough dataset, I don’t see why you couldn’t first find the most similar N cases, and then do a regression with just those cases to make a prediction for a particular observation.  More advanced versions of this could also add some expected error to the prediction.

Self Organizing Maps (SOM)

The goal of the** Self Organizing Maps** (SOM) is to use unsupervised machine learning to represent complex data in a low (e.g, 2D) dimensional space.  They are actually types of artificial neural networks (ANNs), meaning that we are going to be talking about nodes, and a set of weights for each node, and our algorithm is going to find the optimal weights.  If you have ever seen the reference to a “Kohonen” map or network, this is talking about the same thing, and just giving credit to the guy that came up with them, Mr. Teuvo Kohonen.

How to Build a SOM

As with many algorithms, building a SOM involves training, and then mapping (or classifying a new input).  Training comes by way of vector quantization.  You can imagine that we start with a random set of centroids, and at each iteration, we select a point and find the centroid that it is closest to, and move that centroid a tiny bit toward the point. And after many iterations, the grid does a good job of approximating the data.  An example (from wikipedia!) is shown below:

In the case of SOM, these “centroids” are called nodes or neurons, and with each node is an associated vector of weights.  This vector of weights is nothing more than the current vector of feature values for the centroid.  The simplest SOM algorithm starts with this vector initialized to be random, but there are better ways.  Generally, training works as follows:

1. Initialize weights
2. Prepare your points to feed to the network!

For each point {

1. Calculate the euclidian distance of the point to all nodes in the network.  The closest one is called the “Best Matching Unit” (BMU)
2. Adjust the weights of the BMU toward the input vector, as well as other points close in the SOM lattice (“close” as determined by some neighborhood function, a Gaussian function is a common choice)  This neighborhood function should shrink with time so the weights converge to local estimates.

}

You would need to do this for many points, of course.  At the end of your training, each node should be associated with some pattern in the data.  To classify a new point, simply calculate its Euclidian distance to all nodes in the space, and the closest one wins.   SOMs are cool because they are sort of like a non-linear form of PCA.  Another way of achieving this goal is by way of multidimensional scaling, which aims to represent observation vectors in a lower space, but preserve the distances between them.

Vector Quantization

Vector Quantization is a method to compress data, and it’s considered a lossy technique because we are creating a new representation for a set of N observations that loses some of our information.  This happens because we represent each of our observations based on a “prototype vector.”  You can think of it like doing k-means clustering, and then representing each observation vector based on its centroid, and throwing away the raw data.  A simple algorithm goes something like this:

1. Divide observations into groups having approximately the same number of points closest to them (or I don’t see why you couldn’t use k-means or some variation of that)

Repeat until convergence {

1. Define a vector of sensitivity values for each centroid (some small value)
2. Pick a sample point at random, find the centroid with the smallest distance - sensitivity
3. Move the centroid a little bit toward the sample point
4. Set the centroids sensitivity to zero so it will be less likely to be chosen again

}

What does convergence mean?  We can use simulated annealing, which broadly lets us find a good global optimum in a search space by temporarily accepting less optimal solutions.  We do this by having a function, P, that takes in the energies of two states (a measure of their goodness) and a “temperature” T, that must start off higher (close to 1) when the algorithm starts, and eventually go to zero.  This function P needs to be positive when our transition state is more optimal than our current state.  When T is large, we are willing to step uphill (because it might be a local optimum!) and when T is small, we only go downhill (we reach the end of our annealing schedule, and are ready to converge to a solution).

In the context of Vector Quantization, using an annealing schedule probably means that we look at training by moving a vector based on one point as a state, and the next state being the next move we make with our next point.  We stop adjusting with new points when some metric (the function P) that evaluates the energy of each state (taking into account our annealing schedule) is less than a randomly generated probability.  See the pseudocode for more clear explanation.

Benefits of Vector Quantization

This is cool because you can see how the densities can easily be updated with live data, and you can also see how we could deal with missing data.  If we match a new point to the closest centroid (based on the information that we do have), we can then ascribe the average of the missing parameters to the data point.

Changes from DSM-IV to DSM-V

The DSM is the Diagnostic and Statistical Manual of Mental Disorders, and is the “gold standard” that clinicians use to make an assessment about an individual.  The DSM-V was published (officially) on May 18, 2013, and while there are many changes to move it from a categorical to a dimensional classification system, it still seems out of date in that it does not reflect the shift in psychiatry to define different disorder based on biological variables (e.g., data!)

Despite my bias that a model of mental disorder based on behavioral observation is, well, bad, I still think that it is important to understand how the manual has changed between these two versions.

Changes in the DSM Between version 4 and 5

• Subtypes of autism (Asperger’s and pervasive developmental disorder not otherwise specified PDD-NOS) went away.  Everyone now falls into one bucket, autism spectrum disorder.
• Subtypes for variant forms of schizophrenia have also gone away.
•  New “disorders” include gambling disorder, tobacco-use disorder, premenstraul dysmorphic disorder, and caffeine addiction - see here for a nice summary.
• “Disruptive Mood Dysregulation Disorder” is to replace pediatric diagnoses of Bipolar
• The multi-axial system of diagnosis has been dropped
• Global Assessment of Functioning (GAF) has been replaced with the World Health Organization (WHO) Disability Assessment Schedule
• “Panic Disorder” and “Agoraphobia” are now two separate disorders
• “Separation anxiety disorder” and “selective mutism” are now types of anxiety disorder
• Lots of excitement in the OCD department!  We have four new disorders: 1) excoriation (skin-picking) disorder, 2) hoarding disorder, 3) substance-/medication-induced OCD, and 4) OCD due to another medical condition.
  
• Subtypes of gender identity disorder based on sexual orientation - finally deleted

This of course isn’t a comprehensive list, but it seems to be the “biggest stuff,” imho.

Modularity Optimization Algorithm of Newman

When we create a network, we are concerned about how the components are broken into groups, and how those groups are connected.  This is relevant to graph theory, where the basic idea is to have entities in some system represented as nodes, and the relationships between them (some similarity metric) represented as connections between the nodes (called “edges”).  The way that one of these graphs is built typically goes something like this:

1. For n observations, create an n x n similarity matrix S, where each box Sij represents the similarity between observation i and observation j
2. Threshold the matrix at some meaningful value so that boxes above the threshold become nodes of the graph, and boxes below the threshold go away

This is very simple, and how I’d probably do it.  And I’d probably choose a threshold so that each node has minimally one vertex, because we don’t want any lonely nodes floating off by themselves.  But if we read more about graph theory, once we have some set of nodes and vertices, how do we define the groups?

We define groups to maximize community structure

The idea of community structure says that there are groups of highly connected observations, and the connections between these groups are pretty sparse.  In the domain of neuroscience, this community structure would be coined a “small world network,” relevant to a disorder like autism, as it has been propose d that the autistic brain is defined by these small world networks.

The concept of **modularity **is the number of connections (edges) falling within groups minus the expected number in an equivalent network with randomly placed edges.  This means that modularity can be positive or negative, and if it’s negative, this hints at the graph having community structure, because there are relatively more edges.

This is pretty simple, but when I was thinking about graphs, I asked the question, “How do we know how to define groups?”  This post will discuss one simple method proposed by Newman.

Newman’s Modularity Optimization Algorithm

Newman basically takes the modularity matrix, defined as:

where Aij is the adjacency matrix, and each box has the number of connections between vertices i and j (in this case, this will be 0 or 1).  ki and kj are the degrees of the vertices, and m is the total number of nodes in the network.  The modularity, then, is the sum of all of these values for all pairs of vertices in the same group.  We can express this as:

The 1/4m (the paper says) is conventional (to go along with previous definitions of modularity), the vector s is a vector of {-1 1} that says if a particular vertex belongs to group 1 or 2, and the matrix B is the modularity matrix we defined above.  Our goal is to maximize this modularity, Q, by choosing the appropriate division of the network, reflected by the vector s.

What Newman does is 1) compute the leading eigenvector (see paper for details),  and 2) divide the vertices into two groups according to the signs of the elements in this vector.  If all the values are positive, this means that there is no division of the network that results in community structure (we call the network **indivisible **in this case).  A larger value means that the vertex in question is a big contributor to the community structure (in other words, you can imagine a large value is spot in the middle of a big cluster, and if we moved it, we’d mess up the group pretty significantly), and a small (positive) value could be moved to a different group with less influence on the network.

What about if we have more than one group? (of course we do!) We apply this algorithm many times: i.e., break into the best two groups, and then break each group into two, and we continue until the signs of the eigenvectors are all positive, meaning that we do not improve community structure by continuing to break.

Another method!

This Newman guy, he is full of ideas - the paper has another method!  We start by diving our vertices into two groups, and then we find the one vertex that, when moved to the other group, results in the biggest increase in modularity.  We then keep making moves with the constraint that no vertex is moved more than once.  When all have been moved, we then have an idea about how salient each one is to the community structure, and we can search around these intermediate states to find the greatest modularity.  We then have a new grouping, and we keep doing this until there is no improvement in modularity.

A Caveat: High Modularity Doesn’t Always Mean Having Strong Community Structure

Well, crap.  Why is this the case?  As our network gets really big, so does the number of possible divisions of that network. In this landscape, it is possible that there exists a division with high modularity and not strong community structure.  This only means that high modularity is necessary but not sufficient for evaluating community structure.  You might also want to use something like VOI, or variation of information.  This basically means doing a random perturbation of your assignments, and then re-assessing the modularity.  The VOI is the difference between the first clustering and the perturbed one.  A graph with true community structure will have little change in VOI because any one vertex movement is not going to significantly alter the true structure.  A graph that has high modularity due to random chance will have a large change in VOI.  You can calculate this metric for different numbers of random changes in assignments and assess the change in the VOI.

Flatten 3D Data to Vector, and back to 3D in R

There is surprisingly little help online about how to flatten some 3D data, and then “unflatten” it back to its original size. Why would you want this functionality? Many machine learning algorithms that work with images treat pixel values as features, and so we represent each image as a vector of image intensities. The output (depending on the algorithm) might be an equivalently sized vector that we want to re-assemble into its previous 3D loveliness.

This is by no means a clever way of doing this, however it works and so I’ll share it. For my specific implementation I am reading in structural brain imaging data (called nifti files), however the 3D data could be of any type. This simply demonstrates the basic functionality – it’s more likely you would read in many files and stack the vectors into a 2D matrix before whatever manipulation you want to do, in which case you can just add some loops :)

# Load nifti library
library('Rniftilib')

# Try loading in a nifti file
nii = nifti.image.read("NDARZW794FK8_anat.nii";,read_data=1)

# For each file, flatten into a vector
niivector = as.vector(nii[,,])

# Create empty array of same size to fill up
niinew = array(0, dim=dim(nii))

# Do some manipulation to vector(s)
# Option 1: Reconstruct 3D image manually
mrcounty = 1
for (i in 1:dim(nii)[3]) {
  niinew[,,i] = niivector[mrcounty:(mrcounty+dim(nii)[1]*dim(nii)[2]-1)]
  mrcounty = mrcounty + dim(nii)[1]*dim(nii)[2]
}

# Option 2: The one line answer
niinew = array(niivector, dim=dim(nii))

# Rewrite the image to file
template = nii
template[,,] = niinew
nifti.set.filenames(template,"C:/Users/Vanessa/Documents/test.nii")
nifti.image.write(niicopy)

Archetypal Analysis

Archetypal Analysis is an unsupervised learning algorithm that postulates that each of our set of observations is some combination of some number, K, “pure subtypes,” or archetypes.  I’ll also refer to these as prototypes.  In the simple case of adult human faces, you can imagine that there might be a prototypical face for each gender and ethnicity, and then every human being can be modeled as some combination of these prototypes.  Similar to non-negative matrix factorization, we start by modeling our data, X, as the result of multiplying some matrix of weights, W, by the prototypes, H:

• X is sized N x p, number of observations  x number of features
• W is sized N x r, number of observations x number of prototypes
• H is sized r x p, number of prototypes x number of features
• We assume that the number of prototypes, r is less than or equal to N, our number of observations.  It makes sense that in the case of r = N, each prototype is just an observation itself!
• The number of prototypes, r, can be greater than the number of features, p.  In the case of faces, this is saying that the number of prototype faces can be greater than the number of pixels in the image.

Since a negative weight doesn’t make much sense, in this algorithm we assume that our weights are greater than (or equal to) zero.  We also assume that, if we sum up a row of weights defining a particular observation, we must get a value of 1.  Intuitively, the weights would be saying “this observation is 50% Prototype 1, 25% prototype 2, 25% protype N, and so adding up all of these weights we want to get a value of 1 (100%).  We can still have some weights set to zero (for example, if there was an alien face prototype in the mix, a human observation would (hopefully) have the weight for this prototype as zero.  We are modeling each of our observations as some convex combination of the subtypes.  We also can say that:

and I (think) that B is akin to the inverse of W, in ICA we would call this the “unmixing matrix.”  The values in this matrix B need to equivalently be positive, and it is size r x N.  Here we are modeling the prototypes as convex combinations of our original data!  That’s pretty neat.  With the two equations above, we can come up with an incredibly simple way to solve for W and B.  Since we want WH (or WBX) to best approximate X, to solve for W and B we can minimize the function that subtracts WH from X.  If X - WH is zero, that means that our prototypes and weights approximate the data perfectly.  As the value gets larger, we obviously aren’t doing as good a job:

The second equation simply comes from substituting in BX for H.  We are taking the L2 norm (the euclidian distance, meaning that we find the difference between each feature vector by subtraction, square this value so it’s positive, and then take the square root of the entire thing.  We minimize this function in an alternating fashion, and while each separate minimization involves a convex optima, the overall problem is not convex, and so we usually converge to a local minimum.

Achetypal Analysis is sort of like K-Means

The picture below shows Archetypal analysis (top row) compared to K-Means clustering (bottom row) on the same dataset for different values of K archetypes or clusters.  What I notice from this is that Archetypal analysis gets at the “extremes” in the dataset (notice how the archetypes, the red points, are around the edges?) while K-means centroids (the blue points) try harder to get the most average representations.  Thank you again to the ESL book for this photo!  Statistics / machine learning / informatics students everywhere are thankful for your loveliness:

With this understanding, how would you hypothesize archetypal analysis would perform when applied to learning a dataset of pictures of numbers?

If you guessed that the resulting archetypes are “extreme” threes, you are correct.  The picture above doesn’t show any “average” looking 3’s: they are all super long, super thin, super fat, etc.  Those are some **extreme 3’s! :)  As is the case for all these methods, I have not discussed how to decide on the number of prototypes, or the number of components.  There are methods to come up with a good number, to be discussed in a different post.

Non-Negative Matrix Factorization

Non-negative matrix factorization (nnmf) is an unsupervised machine learning method for (you predicted it, strictly positive) data!  The goal of nnmf, of course, is dimensionality reduction.  We start with a dataset, X (size N x p), and want to decompose it into a matrix of weights W (size N x r) multiplied by some matrix of components H (size r x p), the idea being that these components are a reduced representation of our original data.  We want the value of WH to do a good job approximating our original data:

Does this look familiar? It is incredibly similar to one of my favorite unsupervised learning algorithms, independent component analysis, for which we equivalently decompose a data matrix, X, into a matrix of weights (A) multiplied by a matrix of components, the “true” signal (s).  The primary difference between these two algorithms is that ICA solves for the components based on the assumption of independence of the components.  In ICA, we are trying to maximize the non-gaussianity of our components (to maximize independence), and this is done, for example, by way of minimizing or maximizing kurtosis, which “gets at” independence,  because the kurtosis of a normal distribution is zero.  I will save discussion of different ways to solve for the weights of ICA for another post.  For now, just know that nnmf does not assume independence of the components.  This gives me a huge sigh of relief, because I never liked this assumption so much, even if it worked well.  The second salient difference from ICA is that, since our data is all positive, our resulting matrix of weights is also positive.

Why am I excited about nnmf?

I have been exploring using ICA not for dimensionality reduction, but for definition of subgroups.  Broadly, I want to look at the mixing matrix as a matrix of weights telling us for any particular observation (a row) the relative contribution of that observation (one of the weights in that row) to each component.  In the case of ICA, you can see how this might not be an intuitive strategy, because we can have negative weights in the mixing matrix.  It makes sense that a weight of zero indicates no contribution, but what about a negative weight?  To prepare the data, the means are subtracted, and so a negative weight does not correspond to somehow being opposite of a positive one, it just indicates being less than one.  That’s kind of confusing.  How do I interpret these negative weights?  nnmf, it seems, is more fit for this sort of interpretation because all the weights are positive.  In this light, nnmf can be thought of as a “soft clustering,” with each weight representing the membership of that observation to the component in question.  That’s super cool!  The data that I’m working with happens to be non-negative (because it represents volumes of different matter types), however nnmf would generally be fantastic for many types of imaging analysis, because color values are not negative.  Anyway, the goal of nnmf is to come up with this matrix of weights, W, and the associated components, H.  How do we do this?  First, a review of our assumptions:

NNMF Assumptions

• As we already stated, the data, X, is all positive
• We still need to choose a value for r, the number of components.  As is true with ICA, r must be less than or equal to the max(N,p) (number of observations, number of features)

Solving for W and H

We want to maximize the following equation:

This is derived from a poisson distribution with mean (WH)ij.  If you look at the pdf (ok, wikipedia calls it a pmf, that’s fair) for poisson, you will get a sense that the e term goes away when we take its log, and we are left with just the negative lambda parameter (in this case, the negative mean, defined above), and the value of k must be equal to 1, explaining the first term being just the log of the mean.  We then of course multiply each of our xij by the pdf/pmf, and multiply over all features and observations, to get the likelihood.  However, we don’t see a product above because this is a log likelihood, meaning that we’ve taken the log of both sides.  As a reminder, we do this because it transforms the product into a nice sum, and so if any one of our values is zero, that doesn’t mess up the entire calculation.

How does it compare to other dimensionality reduction methods?

Here is where it gets cool, and I must note that I’m taking these pictures from The Elements of Statistical Learning, v.10.  NNMF was compared to standard principal component analysis, and vector quantization (comparable to K-means) using a large database of picture’s of people’s faces.  Each method “learned” a set of 49 “basis” images (shown below), and the cool part is that the basis images of NNMF turn out to be parts of faces:

(from ESLv.10!)

Red indicates negative values, and black positive.  The big matrices on the left are the components, while the middle matrix represents the weights, and when you multiply them you get a reconstructed representation of the original data.

Problems with NNMF - the solution is not unique

Ah, so it’s not perfect.  The biggest problem is that the decomposition may not be unique.  The vectors that we choose to project our data onto can be anywhere between the coordinate axes and the points, and so we are biased based on our starting values.  Thank you, page 556 of ESL for illustrating this point in the case of two dimensional data:

Problems with NNMF - we still need to choose a value for r

In the simplified explanation above, we start with a chosen value of r.  As with ICA, there are approaches (such as FastICA) that can be used to approximate the dimensionality, and I bet that we can do something similar for NNMF.  I need to think about this, and do more reading.

Sparse K-Means Clustering "Sparcl"

Tibshirani and Witten introduced a variation of K-Means clustering called “Sparcl.”  What gives it this name?  It is a method of sparse clustering that clusters with an adaptively chosen set of features, by way of the lasso penalty.  This method works best when we have more features than data points, however it can be used in the case when data points > features as well.  The paper talks about the application of Sparcl to both K-Means and Hierarchical Clustering, however we will review it based on just K-Means.  We will start with doing what the paper does, which is reviewing previous work in sparse clustering. Previous Work in Sparse Clustering

• Dimensionality Reduction Algorithms: 
• Use PCA to reduce the dimensionality of your data, and cluster the reduced data
• Use Non-Negative Matrix factorization, and cluster the resulting component matrix

What are the problems with the dimensionality reduction proposals above?  They don’t allow for sparse features, and we cannot be sure that our signal of interest is in the resulting decomposition.  Why?  The components with the largest eigenvalues do not necessarily do the best to distinguish classes.  Let’s talk about other ideas.

• Model-based clustering framework: 
• Model the rows of the data, X, as independent multivariate observations from a mixture model with K components, and fit with the EM model.  The picture below  shows this approach:

The function, fk is a is Gaussian density, and it is parameterized by its mean and covariance matrix.  We iterate from 1 to K in the inside loop, one for each Gaussian, and the outside loop from 1 to n is going through each of our data objects.  Fitting with EM means fitting by expectation maximization.  The problem with this algorithm for this application is in the case when our number of features (p) is much bigger than our number of observations (n).  In this case, we can’t estimate the p x p covariance matrix.  There are ways around this (see paper), however they involve using dimensionality reduction, and the resulting components, in being combinations of all features, do not allow for sparsity.  Poozle.  Is there another way we can use model-based clustering? Yes.

• Use model-based clustering (above), except instead of maximizing the log likelihood, maximize the log likelihood subject to a penalty that will enforce sparsity.  What does that look like?

Above, you will see the same equation as before except… oh hello, L1 penalty!  The last double summation above is basically summing up the means for each feature (j) across all Gaussians (k).  The parameter out front, lambda, is a fudge factor that gives us some control over the penalty.  When lambda is really big, this means that we are penalizing more, and so some of the Gaussian means will be exactly equal to zero.  When this is the case for some feature, j, over all Gaussians, K, this means that we don’t include the feature in the clustering.  This is what makes it sparse.    It isn’t clear in the paper why this approach isn’t sufficient, but let’s move into their proposed “Sparcl.”

Sparse Clustering, Sparcl

Let’s start simply, and generally.  Unsupervised clustering problems are trying to solve the following problem:

Xj denotes some feature, j, and so the function is “some function” that involves only the j-th feature.  We are trying to maximize our parameters for this function.  For example, for K-Means, this function is the between cluster sum of squares for feature j.  The paper proposes sparse clustering as the solution to the following problem:

The function, f, is the between cluster sum of squares, j is still an index for a particular feature, and wj is the weight for that feature.  We can say a few things about the equation above:

• If all of our weights are equal, the function above reduces to the first (without the subject to addition) and we are using all features weighted equally.
• s is again a tuning parameter.  When it is small, this means that we are more stringent, and more of our weights will be set to zero.
• The L2 norm, which means that we square each weight, sum the squares, and then take the square route of that, is important as well, because without it, at most one weight would be set to zero.
• The value of the weights, as usual, is reflective of how meaningful a particular feature, j, is to the sparse clustering.  A large weight means that the feature is important, while a small one means the opposite.  A weight of zero means that we don’t use it at all.  Dear statistics, thank you for making at least one thing like this intuitive!
• Lastly, the last term in the “subject to” says that we can’t have all of our weights equal to zero, in which case we have no selected features at all!

How do we solve the equation above?  We first hold our weights, w fixed, and optimize with respect to the parameter.  We then hold our parameters fixed, and optimize w.  The paper notes that when we hold the parameters fixed and optimize w, the problem can be rewritten as:

For the above, the “subject to” parameters are equivalent, and since our parameters are fixed, we are just multiplying the weights by a, where a is a function of X and the fixed parameter.  The paper notes that this can be solved with soft-threholding, something that I need to read up on.  It is detailed in the paper if you are interested.  Now let’s talk about this approach specifically applied to K-Means.

Sparse K-Means Clustering (Sparckl?) :)

This is going to be a good method for three reason:

1. the criteria takes on a simple form
2. easily optimized
3. the tuning parameter controls the number of features in the clustering.

Let’s first talk about standard K-Means.  For standard K-Means, our goal is to minimize the within cluster sum of squares (WCSS). This means that, for each cluster centroid, we look at the points currently assigned to that cluster, square each one, and add them up.  If this value is small, our cluster is tight and awesome.  The equation below is saying exactly this:  on the inside we calculate the distance between each cluster centroid and each member across all features j, and then we make sure to divide by the number of members in the cluster (nk) to normalize for differences in cluster sizes.  We then add up the summed distances for each cluster, K, to get a “final” total distance.

We want to minimize this total distance to yield the “tightest” clusters, i.e., the clusters that have their points closest to their centroids.  The equation above uses all features, j, and so there is not sparsity.  Before we add a penalty and weights, let’s talk about the between cluster sum of squares, BCSS.

The term on the right is exactly what we had before, the within cluster sum of squares for all clusters K.  However, what we are trying to get at is the between cluster sum of squares, meaning that we want to minimize the distance between all the points in a cluster and all the other points not in the cluster.  So the equation above, in the first term that does not take a cluster k into account, is basically saying “ok, let’s imagine that we don’t have any clusters, and just calculate the pairwise distance for all of our observation, n, and then get an average.   We can then subtract the within cluster sum of squares, leaving only the distances for the pairs of points from different clusters.  The between cluster sum of squared distances.  And we do this for all of our features, p.  Maximizing the between cluster sum of squares (above, meaning that points in different clusters are far apart) is equivalent to minimizing the within cluster sum of squares.

Now, let’s add weights and penalty terms!  The paper notes that if we were to add these parameters to the equation that just specifies the WCSS, since each element of the weighted sum is negative (see that big negative sign in front of the WCSS equation?) this would mean that all of our weights would be zero. Fail!  Instead, let’s add the weights and penalty terms to the BCSS equation:

The Sparse K-Means Clustering Criterion

Holy crap, that looks ugly.  But it’s really not as scary as we think - all that we’ve done is taken the BCSS equation from above, and appended a weight (w) to the front for each feature, j.  As before, we can say some things about this criterion:

• When the weights are all equal, we are back to basic BCSS
• The smaller s, the more sparse the solution

Intuitively, we are assigning a weight to each feature, j, based on the increase in BCSS that the feature can contribute.  Why does this make sense? If BCSS is greater, we would want our weight to be larger to result in a larger value.  If BCSS is smaller, we don’t get so much out of the feature, and since we are constrained in our values for w, we choose a smaller w and (hopefully) other features will be more meaningful.

How to use the criterion to solve for the optimal weights

1. Initialize each weight equal to 1/sqrt(p)
2. Iterate until convergence {

Forget about the first term in the BCSS equation, and just think of standard K-Means.  Our first step is to minimize the WCSS for our current (fixed) weights:

This is how we are going to come up with our cluster assignments and centroids - we want points getting matched to their closest centroid, and on each iteration we re-define the cluster centroids based on the assigned points.  Yes, this is standard K-Means, out of the box!

When we finish with the above, we have defined our centroids, cluster member indices, and this selection has resulted in a minimum WCSS distance.  We now hold these cluster assignments fixed (C1 to Ck), and can look at the left side of the BCSS equation.  As was stated previously, we want to maximize this, and we are going to use something called “soft thresholding.”  Again, see the paper, I will try to discuss soft thresholding in another post.  This results in a new set of weights.  We then define a stopping criterion (below), and keep iterating through these two steps until this stopping criterion is reached:

wr refers to the set of weights obtained at some iteration r, so we are stopping when the change in these weights from one iteration to the next is tiny.  Yes, this is convergence.

}

Further Comments

• Convergence is usually achieved in 5 to 10 iterations
• The criterion is not convex, so we aren’t guaranteed to converge to the global optimum
• We still have to choose our value of K
• To calculate the value of s, we can evaluate the objective using a subset of values of s, and use something akin to a gap statistic:

where O(s) is the objective evaluated at the value of S, and each B is a permuted subset of our data.  We want to permute our data so that our features are uncorrelated.  We choose the value of s with the largest gap statistic.

Why have clinical decision support systems (CDSS) not worked?

This is by no means an all encompassing list, but I wanted to have a place to jot down some ideas for why CDSS are largely just mediocre.  The big picture summary is that there are problems with the models to base the decisions on, access to quality, well organized data, a lack of standards for driving the CDS, and an ability to well integrate them into current hospital systems and workflows.  Specifically:

Our models of disease aren’t good enough:
if we are making decision support for Rx and we still have not identified the correct representation of a disease, how can we predict it?

The data isn’t there / not accessible:
There are privacy issues, or infrastructure of hospital that the system will be used in is not setup to allow for connection and use of relevant data sources

Lack of communication between developers and users:
leading to a system that doesn’t fit in with clinical workflow

Integration with current hospital systems:
A CDS system can only work in practice when it is wellintegrated with existing medical information systems

Lack of standards: 
Good CDSS are reliant on having standards for data, information models, language, and methods for referencing them. For example,

• Medications: RxNorm
• Information models: HL7
• Patient Data: some virtual medical record? (vMR)
• Approaches for terminology / ontology inferencing (OWL)
• and of course, Arden Syntax for taking data –> executable model

The Arden Syntax

What is the Arden Syntax?

• “A standard for representing clinical and scientific knowledge in an executable format.”*

• The goal of the Arden Syntax is to be a standard programming language for the implementation of clinical decision support systems.
• It gets its name from a place called the “Arden Homestead” in New York, where it was prepared in 1989.
• It was first published in 1992 by this group called “The American Society for Testing and Materials,” and was later on integrated into HL7.
• It is now maintained by the HL7 organization, which means “Hospital Level 7” because level 7 is the applications layer of the OSI model.
• You could use it to create decision support systems that qualify as demonstrating “meaningful use.”

Advantages

• it is an actively developed HL7 standard
• it is made with the goal of being readable by a human
• it has measures for time and duration, important in medicine  (specifically each data item in th syntax has two components, the value and primary time)
• it has nice list handling

Challenges / Disadvantages

• integration with current hospital systems
• lack of standardized vocabularies and patient data schemas
• difficulties providing actions for clinicians to take
• lack of up to date tutorials and manuals
• The curly braces problem: in an MLM, curly braces are used to signify parts of the MLM that are specific to the surrounding health IT system. These fragments would need to be customized for each implementation, and this is why we can’t just have a central repository of MLMs for all institutions to use.

How is the code organized?

Into THREE modules, called the “Medical Logic Modules (MLMs) that are each self-contained files.  The execution or “trigger” of these files can be based on data or time-based events, or directly by a person. A MLM can also trigger other MLMs.

What does an MLM look like?

The image below is an example of an MLM, written in Arden syntax, to calculate BMI given an individual’s size, weight, and birthdate.

What kinds of MLMs are there?

There are three categories of MLMs:

• Maintenance: contains metadata about the MLM (author, creation date)
• Library category: background information (references, goals of MLM)
• Knowledge category: contains actual algorithms, database parameters, when the MLM should be triggered etc.  Three sub categores are evoke, logic, and action, i.e., when to evoke, what to do, and what output to produce

How would I use this?

1. You would use an Arden Syntax IDE to write MLMs
2. You would compile with the IDE, producing Java classes out of MLM code
3. You would then use an Arden Syntax Rule Engine to execute the compiled MLMs
4. This rule engine can come by way of an Arden Syntax Server

What are examples of implementations of Arden Syntax?

• HEPAXPERT: Checking and interpreting hepatitis A,B, and C serology (meaning studying blood serum) test results, by way of a web interface or an API. They were able to integrate this into several hospital systems, and an expected ipad/iphone app! (Hepaxpert)
• THYREXPERT: interprets thyroid test results
• TOXOPERT: assist in the interpretation of time sequences of toxoplasmosis serology test results
• Moni-ICU: (monitoring of nonsocomial infections in intensive care units): detects and continuously monitors hospital acquired infections
• Reminder Applications: reminder applications (in use in some VA hospitals) include reminders for eye exams,vaccinations, and  mammograms.  A single MLM is associated with each reminder.

The Future?  libraries of MLM syntax (akin to the Apple App store) for download and use!

Install R Packages (that require compilation) on Linux

When trying to install packages in R that require compiling on one of my servers (that I did not have admin access to) I ran into the following error:

ERROR: 'configure' exists but is not executable -- see the 'R Installation and Administration Manual'
</pre>



The problem here is that the temporary directory that R is clunking the files to be compiled does not have permissions set to execute. To fix this problem, I needed to do BOTH of the following (it doesn’t work without both)

**1. Create a folder somewhere that you do have power to write/execute, etc.**



mkdir /path/to/folder
chmod 777 /path/to/folder



You can undo these permissions later if it makes you anxious.

**2. Set the TMPDIR variable in your bash to this folder:**


export TMPDIR=/path/to/folder



**3. Start R, and install the library “unixtools” that will give you power to set the temporary directory:**


install.packages('unixtools')



Note that you can see the currently set temporary directory with tempdir(). Before changing it, it will look something like this:


[1] "/tmp/RtmpQrgNII";



**4. Use unixtools to set this to a new directory:**


library('unixtools')
set.tempdir('/path/to/folder')
tempdir()
[1] "/path/to/folder";



Now you should be able to install packages that require compilation. At least, it worked for me!

Bootstrapping

Bootstrapping is another strategy (like cross validation) that we can use for validation or parameter estimation if there is not enough data.  The technique is simple: we basically do random sampling from the original dataset to generate a larger dataset that we can either estimate some population parameter from, or use to train a model.   I (think) that bootstrapping is most commonly used to estimate standard errors of predictions (as outlined below).

1. Sample N times randomly from our training dataset to make a “bootstrap” dataset
2. Estimate your model on the bootstrap dataset
3. Make predictions for the original training set

Repeat many times and average your results (accuracy, error, etc).  You could also do a modified version that estimates errors using the samples not included in the bootstrap dataset.  To do this you would simply need to keep track of who was picked each time, and then use a set difference function with that list and the original training set to get who was not included. (Matlab function is setdiff)

Standard Errors and Confidence Intervals

I’ve been reading over beautiful notes from STATS315A (thanks to my awesome fellow graduate student Katie!), one of the three statistics courses I wanted to take, but haven’t been able to squeeze in (yet!)   The course notes provide beautifully clear explanations of very common concepts.  Specifically for this post, we will review standard errors and confidence intervals.

The standard error of an estimate is the standard deviation.  it’s called “standard error” because in most cases we don’t actually know this value, and so we estimate it.  This estimate is called the standard error (se).

We estimate the variance (the top term) by:

A confidence interval lets us say that we are some percentage confident that our parameters fall in a specific interval.  This reflects the quality of our estimates.  It is common to use a 95% confidence interval, and we get it by adding/subtracting 1.96 multiplied by the standard error of our estimates (defined above), i.e.,:

Hierarchical Clustering

Hierarchical clustering is a clustering algorithm that aims to create groups of observations or classes based on similar features, x.  It is commonly used for microarray or genetic analysis to find similar patterns of expression, and I’m sure that you’ve seen its “tree” output in some paper (this tree is called a dendrogram).

Here we see experiments across the top, and genes down the side.  By doing these two separate clusterings and then sorting in both dimensions, we can see patterns emerge in the data.  This is a nice way to visualize patterns in data with many features.

Kinds of Hierarchical Clustering

There are two kinds of hierarchical clustering.  Bottom up algorithms start with each data observation in its own cluster, and then sequentially merge (or agglomerate) the two most similar clusters until one giant cluster is reached.  Top down algorithms start with all of the data in one giant cluster, and recursively split the clusters until singleton observations are reached.  In both cases, you can then threshold the clustering at different levels (think of this like snipping the tree horizontally at a particular level) to determine a meaningful set of clusters.  Agglomerative (bottom up) hierarchical clustering is much more common than divisive (top down), and will be the primary topic of this post.

Agglomerative Hierarchical Clustering (HAC)

Since we will be starting with singleton observations and merging (bottom up!), we need some criteria for assessing similar observations.  Then, when we construct our tree, the y axis values will be our similarity metric, and we can start from the bottom and walk up the tree to reconstruct the history of merges.  For most implementations of HAC, at each step we choose the best merge(s).  A nice fact about this algorithm is that you don’t need to specify the number of clusters, as would be necessary in something like k-means.  You can run the clustering, visualize the dendrogram, and then decide how to cut the tree.  There are a few ways to decide on where to cut the tree:

• Cut at some threshold of similarity.
• Cut where the gap between two successive merges is the largest, because this arguably indicates a “natural” clustering.
• Decide on a number of clusters, K, that minimizes the residual sum of squares.  Specifically:

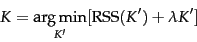
You can think of the second term as adding a penalty for each additional cluster, and this of course is based on the assumption that fewer clusters is better.

How is it commonly implemented?

Given N observations, the first step is to compute an NxN similarity matrix using your similarity criteria.  You then go through iterations, and at each iteration, merge the two most similar clusters and update your similarity matrix with this merge.  If we are doing single-link clustering then we assess the similarity of the closest observations in two clusters, and if we are doing complete-link clustering then we assess the similarity of the most dissimilar members of the two clusters.  You can imagine that single-link will result in long, straggly clusters, while complete-link results in tighter clusters with smaller diameters.  You could also do centroid clustering which evaluates the similarity of two clusters based on the distance of the centroids.

Markov Decision Processes

To talk about Markov Decision Processes we venture into Reinforcement Learning, which is a kind of learning that is based on optimization using a reward function.  For example, let’s say that we are training a robot to navigate a space without bumping into things.  Unlike with supervised learning where we have a clear set of labels that we want to derive, in this problem we have many potential states for the robot (moves it could make, places it could be), and so the idea of having concrete labels doesn’t make much sense at all.  However, we can come up with a function that represents the goodness of some state (the reward function).  Using this function, we can give the robot points when he makes a move that we like, or take away points when he does something stupid (e.g., bumping into something!).  Our learning algorithm, then, will figure out the optimal actions to take for the robot over time to maximize this reward function.

Reinforcement learning is based on the Markov Decision Process

We will model our world as a set of states (S), actions (A), a reward function (R), and what are called transition probabilities (P), or the probability of transitioning to any particular combination of state and action from a particular state and action.  We start in some state, s-0, and take an action, a-0, based on the transition probabilities of that state, and then we arrive in a different state, s-0, and take a different action, etc.

Optimization starts with a reward function, R(s,a)

Given that there is some reward (good or bad) associated with each of our decisions, it makes sense then, that the total reward of all of our decisions is a function of each action / state pair:

The extra parameter is intended to apply a “discount factor” to time, in the case that we need to discount rewards that are farther in the future.  Because we are stubborn and impatient and want things… now! :)  So, the goal of our learning algorithm is to maximize the expected value of the equation above.  Let’s call the value that we get starting at some state, s, a function V(s).  It makes sense, then, that the expected reward starting at this state s is:

1. the reward that we get in the current state PLUS
2. the sum of the (discounted) rewards of all future states

We can write this as:

We could write an equation like this to model different possible combinations of states / actions, and we can define the optimal value function as the combination of states with the best V(s), meaning the highest possible reward:

This policy is optimal no matter what our starting state is.  Now, how do we find it?

We optimize the value function with value iteration

**This only works given that there is a finite number of states and actions, which seems reasonable for most learning problems.  The algorithm works as follows:

1. Initialize V(s) =0 for every finite state
2. Repeat until convergence {

For every state, update:      
}

The two algorithms, (and I’m not sure which is better), are generally the above, value iteration, and there is also policy iteration.

For value iteration, we would want to solve for the optimal value function (above), and then plug this value into the equation below to find the optimal policy:

In the case above, we knew the transition probabilities in advance, however keep in mind that it’s common to not know these probabilities, in which case you would need to update these transition probabilities before calculating the value function in each loop as follows:

and in the case that we get an undefined / NaN 0/0 it’s best to have the probability equal to .

This isn’t a completely satisfactory explanation of the algorithm, and that is because I haven’t used Markov Decision Processes in my own research (it’s more suited to robots and that sort of thing).  However, when I do I will update this post!