vsoch

Locally Weighted Linear Regression

Let’s say that we have some relationship between our outcome variable (y) and one or more predictors (x) that isn’t cleanly linear, quadratic, or even cubic.  Let’s say that this relationship looks like a squiggle of pasta, and we might keep adding features to get a more squiggley curve, but then we run the risk of overfitting to this particular dataset.  How do we make predictions about values in this case?

We want to use locally weighted linear regression, which is a non-parametric regression method that is sort of like the love child of linear regression and k nearest neighbor clustering.  Non-parametric means that we can’t just derive an equation and throw away the data.  The model depends on the data in that whenever we want to classify a new point, we do so based on the most similar points in our dataset.  You can think of locally weighted linear regression as equivalent to linear regression, except when we minimize our least squares cost function to solve for our parameters, we give more weight to points in our dataset that are similar to the point we are trying to predict.  How does it work?

As a reminder, in linear regression we want to minimize the least squares cost function:

With locally weighted regression, it is exactly the same, except we have a vector of weights:

And we generally define the weights to be the distance of each point to our current x(i):

Incorporating this w(i) means that θ is chosen giving a higher weight to the errors on training examples close to our current x(i).  The “tau” symbol is the bandwidth, which you can think of as a parameter to fiddle with that controls the distance from the query point to define “close” neighbors.

Neuroanatomy of Autism

This article can be found at: http://www.ncbi.nlm.nih.gov/pubmed/18258309

sMRI

• Pathological / abnormal regions in ASD: frontal lobes, amygdala and cerebellum
• time course of brain development, not final product, is most disturbed in autism (so age is a salient factor, and we would want to assess if similar age = more similar brain)
• Kanner’s asd features include: - impairments in reciprocal social interactions
• abnormal development and use of language
• repetitive and ritualized behaviors and a narrow range of interests

Behavior –> Regional Structural/ Functional Abnormality

These findings in the literature pertain to regional aberrancies associated with different behavioral types.  I would want to validate these associations in my work, or use them to quasi-validate my approach.  Broadly, these regions include the frontal lobe, the superior temporal cortex, the parietal cortex and the amygdala.

Language Function

• Expressive language function: Broca’s area in the inferior frontal gyrus and portions of supplementary motor cortex
• Receptive language function: Wernicke’s area,
• Superior temporal sulcus (language processing and social attention)

Repetitive and Stereotyped Behaviors

• share many similarities with abnormal actions of OCD
• regions include orbitofrontal cortex, caudate nucleus
• evidence for enlargement of the caudate nucleus: correlated with the presence of repetitive and ritualistic behaviors in adolescents and young adults?

Amygdala

• boys with autism: appears to undergo an abnormal developmental time course (precocious enlargement that persists through late childhood)
• 13%–16% abnormal enlargement of the amygdala in young children with autism (36–56 months of age)
• amygdala enlargement is associated with more severe anxiety and worse social and communication skills
• neurons in certain nuclei appear unusually small and more densely packed than in healthy control

Epilepsy (highly comorbid with OCD)

• associated with pathology of cerebral cortex, amygdala, cerebellum, hippocampal formation

Brain Size

• young children with autism (18 months to 4 years) have a 5%–10% abnormal enlargement in total brain volume, not clear if persists into adulthood
• Herbert et al. postulated that abnormal brain enlargement in children with ASD is disproportionally accounted for by increased white matter, not gray matter, although gray matter is also increased too

###

DTI

• Reductions in FA in cerebral white matter, consistent reductions reported in and near the genu of the corpus callosum
• DTI and volumetric study of the corpus callosum found a 14% reduction in corpus callosum size was associated with reduced FA in the genu and splenium
• Most consistent increases in gray and white matter have been reported in the frontal lobes, but there is no consistent pattern

An informatics opportunity!

“A perusal of this literature emphasizes the need for the field of developmental neuropathology to establish a systematic approach to evaluating abnormal brain development”

###

Morphometry

• Abnormalities in cortical shape: sylvian fissure, superior temporal sulcus, intraparietal sulcus and inferior frontal gyrus
• cortical thickness, increased over the entire cerebral cortex, most prominent in parietal and temporal regions
• (postmortem) findings: irregular laminar patterns, esp anterior cingulate cortex, increased cortical thickness, high neuronal density, neurons preset in the molecular layer
• abnormalities within the hippocampus, both in volume and shape

Why would neurons be in the molecular layer? or increased neurons in white matter?

###

Microstructure of Cortex

• Cortical layer III: reduced intercolumnar width of the minicolumns in dorsolateral prefrontal cortex or Brodmann’s area (BA) 9
• 79% post-mortem studies show decreased density of Purkinje cells, particularly in the hemispheres, but these subjects also had comorbid seizure disorders, those medications are known to kill these cells
• no postmortem evidence for abnormalities in the thalamus, basal ganglia

It would be worth looking up or assessing if there is abnormal (functional) connectivity with thalamus

Maximum Likelihood Estimation (MLE)

Maximum Likelihood Estimation is a technique that we use to estimate the parameters for some statistical model.  For example, let’s say that we have a truckload of oatmeal raisin cookies, and we think that we can predict the number of raisins in each cookie based on features about the cookies, such as size, weight, etc.  Further, we think that the sizes and weights can all be modeled by the normal distribution.  To define our cookie model, we would need to know the parameters, the mean(s) and the variance(s), which means that we need to count the raisins in each cookie, measure them, weigh them, right?  That sure would take a long time!  But we have a group of hungry students, and each student is willing to count raisins, measure and weigh one cookie, ultimately producing these features for a sample of the cookie population.  Could that be enough information to at least guess the mean(s) and standard deviation(s) for the entire truckload?  Yup!

What do we need to estimate parameters with MLE?

The big picture idea behind this method is that we are going to choose the parameters based on maximizing the likelihood of our sample data, based on the assumption that the number of raisins, height, weight, etc. is normally distributed.  Let’s review what we need in order to make this work:

• A hypothesis about the distribution.  Check! We think that our raisins and other features each are normally distributed, defined by a mean and standard deviation
• Sample data.  Check!  Our hungry students gave us a nice list of counts and features for a sample of the cookies.
• A likelihood function: This is a function that takes, as input, a guess for the parameters of our model (the mean and standard deviation), our observed data, and plops out a value that represents the likelihood (probability) of the parameters given the data.  So a higher value means that our observed data is more likely, and we did a better job at guessing the parameters.  If you think back to your painful statistics courses, we model the probability of a distribution with the pdf, (probability density function).  This is fantastic, because if we just maximize this function then we can find the best parameters (the mean and standard deviation) to model our raisin cookies.  How do we do that?

What are the steps to estimate parameters with MLE?

I am going to talk about this generally so that it could be applied to any problem for which we have the above components.  I will define:

• θ: our parameters, likely a vector
• X: our observed data matrix (vectors of features) clumped together, with a row = one observation
• y: out outcome variable (in this case, raisin counts, which I will call continuous since you can easily have 1/2 a raisin, etc.)

This is clearly a supervised machine learning method, because we have both an outcome variable (y) and our features (X).  We start with our likelihood function:

Oh no, statistics and symbols! What does it mean!  We are saying that the Likelihood (L) of the parameters (θ) is a function of X and y, equal to the probability of y given X, parameterized by θ.  In this case, the “probability” is referring to the PDF (probability density function).  To extend this equation to encompass multiple features (each normally distributed) we would write:

I apologize for the image - writing complex equations in these posts is beyond the prowess of my current wordpress plugins.  This equation says that the likelihood of our parameters is obtained by multiplying, for each feature 1 through m, the probability of y given the feature x, still parameterized by θ.  Since we have said that our features are normally distributed, we plug in the function for the Gaussian PDF.  If you remember standard linear regression, the term in the numerator is the difference between the actual value and our predicted value (the error).  So, we now have the equation that we want to maximize!  Do you see any issues?

I see a major issue - multiplication makes this really hard to work with.  The trick that we are going to use is to take the log of the entire thing so that it becomes a sum.  And the log of the exponential function cancels out… do you see how this is getting more feasible?  We also use a lowercase, italisized script “l” to represent “the log of the likelihood” :

The first line says that we are defining that stuff on the left as the log of the Likelihood.  The second line is just writing “log” before the equation that we defined previously, the third line moves the log into the summation (note that when you take the log of things multiplied together, that simplifies to summing them).  We then distribute the log and simplify down to get a much more feasible equation to maximize, however we are going to take a step further.  If you look at the last line above, the first two terms do not depend on our variables of interest, so we can just look at the last term.

This is equivalent to the cost function that we saw with linear regression!  So we could solve for the parameters by maximizing or minimizing this function.  And does it make sense that you could apply this method to other distributions as well? You would start with their PDFs, take the log of the Likelihood, and then minimize to find the best parameters (and remember to do this we are interested in finding where the derivative of the function with respect to our parameters is zero, because this means the rate of change of the function is zero because we are at a maximum or a minimum point, where the slope is changing direction from positive to negative, or vice versa).  And of course you can get R or Matlab to do all of this for you.  Super cool, no?

Signal to Noise Ratio (SNR)

Sometimes, things are exactly what they seem.  This is one of those cases  The signal to noise ratio (SNR) is a metric that is used in MRI to describe how much of a signal is noise, and how much is “true” signal.  Since “true” signal is what we are interested in and noise is not, the SNR of an image is a reflection of its quality.  A large SNR means that our “true signal” is relatively big compared to our noise, and a small SNR means the exact opposite.

How do we change SNR?

• SNR can be used as a metric to assess image quality, but more importantly, we would want to know how to change it.  Here are a few tricks to increase SNR:
• average several measurements of the signal, because if noise is random, then random contributions will cancel out to leave the “true” signal
• sample larger volumes (increase field of view or slice thickness)… albeit when you do this… you lose spatial resolution!
• increase the strength of the magnetic field (this is an example of the type (i.e., GET A BIGGER MAGNET!)

How do we measure SNR?

I’ve never done this, but I’ve just read about it.  You would want to record signal from a homogenous region with high signal intensity, and record the standard deviation for the image background (outside of your region).  Then calculate:

SNR = Mean Signal/Standard Deviation of Background Noise

When I was more involved with scanning at Duke, we used to have a Quality report generated automatically for each scan that included the SNR.  I would guess that most machine setups these days will calculate it automatically for you.

Partial Volume Effect

Partial Volume Effect in medical imaging speaks to the idea that we may not detect signal in small volumes or regions when our resolution is limited.  If you are a researcher that is totally crazy about the amygdala, for example, you might worry that the limited resolution of MRI would underestimate your signal in functional data.  It also speaks to the idea of losing contrast between two regions (for example, two tissue types within the same voxel) because of such a limited resolution.

I like to think of this second idea, losing contrast between two tissue types because of limited resolution, in the context of multi-ingredient truffles.  Presenting, one of my crazy creations:

The ingredients in these amazing truffles include: dried strawberries, blueberries, crunchy cinnamon apples, raisins, peanuts, coconut, almonds, dates, and walnuts, held together with vanilla touched white chocolate.  How do these delicious bites of glory represent the problem of partial volume effects?  It’s very simple.  Each cluster is akin to a voxel, filled with many different ingredients, but we might be forced to represent the entire thing with only one taste.  We lose information about the different ingredients (the tissue types) because of the limited resolution of our tongue (the imaging modality).

Cross Validation

In a perfect world, we would be able to ask any question that our little hearts desire, and then have available immediately infinite numbers of datasets to test our hypothesis on, and know exactly the model and parameters to use.  Of course, we do not live in such a world, and commonly we approach a problem with:

• not enough data
• no clue about the parameters
• possibly no clue about the model or algorithm to use

Different flavors of cross validation, or a model validation technique that can give us a sense of how generalizable our model is, can help with all of these challenges.  Let’s start with a problem that we face every single day: bed bugs.

Building a Model to Describe Bed Bugs

Let’s say I wake up one morning, and I am shrunk down to the size of an eyelash.  My green bed is a vast landscape covered in, to my horror, a sea of brightly colored bed bugs, chatting and munching on my dead skin, and otherwise having a grand old time.  Also to my horror, some of these bed bugs seem quite ornery, while others seem friendly.  Chatting with a random bug, he tells me that I should be weary of his comrades general mood, because moody bugs tend to bite harder, and so someone with a bed of moody bugs is not going to sleep as well.  Oh dear!  Knowing that I am faced with a once in a life-time opportunity to interact with the bugs, and knowing that moody bugs bite harder, I realize that it would be valuable to predict bug moodiness based on physical features that we might observe with a microscope.  A person who isn’t sleeping well could bring in a pillow with a sample of bed bugs, and the bugs moods could be assessed based on the physical features to determine if they are contributing to the poor quality of sleep.  Knowing that my time as a mini-me is limited and wanting to solve this problem, I decide to collect as much phenotypic data about these party animals as I possibly can.  I approach them randomly and record the color, number of eyes, ears, height, girth, and if the bug is mean or friendly.  I’m lucky enough to get a sample of 100 before whatever spell that shrunk me down runs out, and I am returned to my normal, ginormous human size.

I run to the computer to input my features into a data matrix, with each bed bug in a row, and each feature in a column, and I create a separate vector of “mood” labels to distinguish if the bug was mean (0) or friendly (1).  I hypothesize that I can find patterns in these features to predict the mood, and so I have on my hands a supervised classification problem: predicting mood from phenotype.  It could be the case that particular species of bed bugs associated with a certain phenotype tend to be more or less moody, or it could be that some state of the bug (e.g., a smaller, less well-fed bug) is more ornery than a larger, satiated one.

I decide to try using logistic regression, specifically glmnet, for which I must choose a value of the parameter lambda that controls the sparsity.  (Please be aware that glmnet is best suited for cases when the number of features far outnumbers the number of samples, but let’s just disregard that for the purpose of the example.)  How do I choose this value of lambda?  Let’s define a set of 5 hypotheses, each being glmnet with a different value of lambda (and note that this could also easily be a set of different models that we want to test). If I were to train on all my data and get a metric of accuracy for each hypothesis, if I were to choose the value that minimized this training error, I am taking the risk that the model is overfit to my data, and if presented with novel bed bug features, it would not do very well.  If you remember from my post about the tradeoff between bias and variance, this is called generalization error.  We want to build models that can be extended to data that we have not seen.

Using Cross Validation to Build an Extendable Model

The idea of cross validation is simple.  We are going to break our data into different partitions for training and testing, i.e.,  ”holding out” a subset to test on, and training on the rest.  This will ensure that we can choose the best hypothesis that is not overfit to the training set.  An example cross validation pseudo-code is as follows for our bed bug sample, B:

1. Randomly split B into B-train (70% of the data, 70 bugs) and Bcv (the remaining 30%, 30 bugs).  ”cv” is called the hold-out cross validation set that we will test on.
2. Train each hypothesis (remember our algorithm with different values of lambda) on Btrain only, to get a set of models to test
3. Input the remaining held out 30 bugs (Bcv) into each model and calculate an error
4. Select the model with the smallest error

If we had a tiny amount of data that we wanted to “maximize the utility of” to build a model, we might want to use leave one out cross validation, for which we hold out one data sample, train the model using the other 99, and then test the model on the one sample.  We would iterate through our entire dataset, giving each sample the opportunity to be held out, and each time getting an accuracy assessment (if we were correct or incorrect in our prediction).  When we finished iterating through the entire dataset, we would have a prediction for each sample based on training on the other 99, and we could use these predictions to calculate an accuracy.

Another common flavor of cross validation is ten fold cross validation, for which we break the data into ten equally sized partitions, and iterate through the partitions, training on 9, and testing on 1.  This is also called k-fold cross validation, when k is defined as the size of the partition.  But people choose k=10 quite a lot.

It’s important to have CV and test data!

If you use cross validation to build a model, you should also have another separate dataset to test your model on after cross validation, because the cross validation can bias your resulting parameters.  It will also further show how awesome your model is in that it is extendable to even more data.  This test set is more convincing than using CV alone because it is an independent assessment of your model.

Summary of Cross Validation

From the above, you can see that by testing on data that we did not train on, we get a better estimate of the model’s generalization error, and if we aren’t sure about a particular parameter or model to use, we can pick the one with the smallest generalization error without worrying that it is overfit to our training data.  Sometimes people lik to choose the model or parameter in this way, and then re-train using all of the data.  In this particular case, I will be able to sleep at night knowing that I have best modeled predicting bug mood from phenotype.  That is, if my bugs aren’t particularly moody :)

Independent Component Analysis (ICA)

I’m sure that you’ve heard of the cocktail party problem. The simplest version of the problem posits that you have two people talking in a room with two microphones, each recording a mixed signal of the two voices. The challenge is to take these mixed recordings, and use some computational magic to separate the signals into person 1 and person 2. This is a job for independent components analysis, or ICA.  ICA is only related to PCA in that we start with more complex data and the algorithm finds a more simplified version.  While PCA is based on finding the main “directions” of the data that maximize variance, ICA is based on figuring out a matrix of weights that, when multiplied with independent sources, results in the observed (mixed) data.

Below, I have a PDF handout that explains ICA with monkeys and looms of colorful strings.  I’ll also write about it here, giving you two resources for reference!

What variables are we working with?

To set up the ICA problem, let’s say we have:

• x: some observed temporal data (let’s say, with N timepoints), each of M observations having a mix of our independent signals.  x is an N by M matrix.
• s: the original independent signals we want to uncover.  s is an N x M matrix.
• A: the “mixing matrix,” or a matrix of numbers that, when multiplied with our original data (s), results in the observed data (x). This means that A is an N by N matrix. Specifically,

x=As

What do the matrices look like?

To illustrate this in the context of some data, here is a visualization of the matrices relevant to functional MRI, which is a 4D dataset consisting of many 3D brain images over time.  Our first matrix takes each 3D image and breaks it into a vector of voxels, or cubes that represent the smallest resolution of the data.  Each 3D image is now represented as a vector of numbers, each number corresponding to a location in space.  We then stack these vectors on top of one another to make the first matrix.  Since the 3D images are acquired from time 0 to N, this means that our first matrix has time in rows, and space across columns.

The matrix on the far end represents the independent signals, and so each row corresponds to an independent signals, and in the context of using fMRI data, if we take an entire row and re-organize it into a 3D image, we would have a spatial map in the brain.  Let’s continue!

How do we solve for A?

We want to find the matrix in the middle, the mixing matrix.  We can shuffle around some terms and re-write x = As as s = A-1x, or in words, the independent signals are equal to the inverse of the mixing matrix (called the unmixing matrix) multiplied by the observed data.  Now let’s walk through the ICA algorithm.  We start by modeling the joint distribution (pdf) for all of our independent signals:

In the above, we are assuming that our training examples are independent of one another.  Well, oh dear, we know in the case of temporal data this likely isn’t the case!  With enough training examples (e.g., timepoints), we will actually still be OK, however if we choose to optimize our final function with some iteration through our training examples (e.g., stochastic gradient descent), then it would help to shuffle the order.  Moving on!

Since we already talked about that x (our observed data) = As = A-1s, let’s plug this into our distribution above.  We know that s = some vector of weights applied to the observed data, and let’s call our un-mixing matrix (A inverse), W.

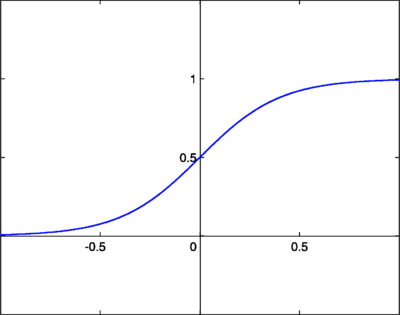
we now need to choose a cumulative distribution function (cdf) that represents the density for each independent signal.  We need a CDF that increases monotonically from 0 to 1, so we choose good old sigmoid, which looks like this:

Now we should re-shift our focus to the problem above as one of maximum likelihood.  We want to maximize the log likelihood parameterized by our mixing matrix W:

Remember that the cursive l represents the log likelihood.  The function g represents our Sigmoid, so g prime represents the derivative of Sigmoid, which gets at the rate of change, or the area under the curve (e.g, density).  By taking the log of both sides our product symbol (the capital pi) has transformed into a summation, and we have distributed the log on the right side into the summation.  We are summing over n weights (the number of independent components) for each of m observations.  We are trying to find the weights that maximize this equation.

Solving for W with stochastic gradient ascent

We can solve the equation above with stochastic gradient ascent, meaning that our update rule for W on each iteration (iterating through the cases, i) is:

the variable in front of the parentheses is what we will call a learning rate, or basically, how big we take a step toward our optimized value after each iteration.  When this algorithm converges, we will have solved for the matrix W, which is just the inverse of A.

Finally, solve for A

When we have our matrix, A inverse (W), we can “recover” the independent signals simply by calculating:

Awesome!

Some caveats of ICA:

There is more detail in the PDF, however here I will briefly cover some caveats:

• There is no way to recover any original permutation of the data (e.g., order), however in the case of simply identifying different people or brain network, this largely does not matter.
• We also cannot recover the scaling of the original sources.
• The data must be non-Gaussian
• We are modeling each independent signal with sigmoid because it’s reasonable, and we don’t have a clue about the real distribution of the data.  If you do have a clue, you should modify the algorithm to use this distribution.

Summary

ICA is most definitely a cool method for finding independent signals in mixed temporal data. The data might be audio files with mixtures of voices, brain images with a mixture of functional networks and noise, or financial data with common trends over time.  If you would like a (save-able) rundown of ICA, as explained with monkeys and looms of colorful strings, please see the PDF below.

Bias and Variance Tradeoff

When we talk about bias vs. variance tradeoff, we are venturing into the field of learning theory that broadly thinks about how to best match particular data to a method, and how to improve performance of a model by understanding the strengths and weaknesses of the methods.

How well does a model fit the data?

When we train a model, meaning an algorithm that predicts some outcome, y, **with features **x, we would be interested to know if our model can be used on similar data, however data that it wasn’t initially trained on.  This extendability of a  model is called it’s generalizability.  Ok, I possibly made up that word - more formally:

• the generalization error is the expected error of a hypothesis on data not from the training set.  The bias of a model is its expected generalization error.
• When a model fits its data too well, we call this this **overfitting. **A model that is overfit to a particular dataset is said to have high variance, and this is a component of (adds to) generalization error.
• When a model does not fit the data well enough, we call this **underfitting.  **

This is a little bit like Goldie Locks and the three bears.  Overfitting and underfiiting are two extremes, and somewhere in the middle, the porridge tastes just right, or we find a model that fits the training data pretty well and can also be extended to data that it has not seen.  This leads to the bias and variance tradeoff:

Bias and Variance Tradeoff

To understand the tradeoff between bias and variance, it’s best to start by looking at the mean squared error (MSE):

The expected mean squared error of our algorithm (subtracting predictions from actual value, squaring), can be broken down into:

1. The variance of the model
2. The squared bias of the model
3. The variance of the error term

Intuitively, to get low error, we need low bias and low variance.  The bias component of the error “gets at” error that is the result of our model choice.  If we have chosen too simple a model and we don’t capture some pattern, the bias is high, and we are under-fitting.  The variance component of the error is about the data, and “gets at” the amount that the error might change if we used a different test set.  Thus, high variance means that if we tested on another dataset, we might get much higher error, and so our model is possibly over-fitting to our training data.  Both of these components get at a models generalization error, which could be high due to high variance and/or high bias.

How do we quantify generalization error?

We quantify the generalizability (not a word!) of a model with the training error, **or empir**ical error, which is the fraction of the samples that the model in question misclassifies.  The generalization error is the probability that a new sample is misclassified by our model.

Empirical Risk Minimization: We can use generalization error to build a model!

Just like we found the best parameters in linear regression by minimizing the sum of squared distances (the residuals, error, etc.) we can tackle the problem of finding optimal parameters for a model by simply minimizing the training error.  This process of finding parameters by minimizing the training error is called empirical risk minimization.  The size of the sample, m that is required for our model to get a particular level of performance is called the algorithm’s sample complexity.

Bias and Variance Tradeoff Relation to MSE

We can see from the above that since neither variance nor bias can be negative, if we decrease one and hold error constant, the error must go up.  This is the bias / variance tradeoff, and it says that when bias is low (we have small prediction error), variance is high (it doesn’t extend as well to different data), and vice versa.

What does overfitting look like?

The best example of overfitting comes by way of an illustration:

We are plotting model complexity on the x axis, (e.g., the number of predictors in a linear regression), and the error on the y axis. The blue line represents our training data, and the red line represents our testing data. For training, we see that as we add more predictors, our model improves.  However, what we are actually doing is fitting the model to noise in the data.   It means that the model performs really well to predict our training set, and does terribly with the test set, which is why there is such a huge distance between the two lines on the right side of the chart.  For testing, we see the error decrease down to a certain point, and then it starts to grow. The area after this “sweet spot” where test error starts to increase is what we call overfitting.  It’s sort of akin to the real world practice of fitting people with mouth guards:

Underfitting: (in other words, not using enough information, and having a model that is too simple all together):  In this scenario, you create a mouth guard out of two strips of plastic in a general half circle shape based on the idea that mouths are kind of shaped like that.  Since you didn’t have enough parameters or good quality information going into the model, it might be the “best” mouth guard to be shared between humans, lemurs, and baboons, but it by no means is a good model for a mouth guard.  This point could be represented somewhere on the left side of the chart above.  Let’s keep moving down the curve to the right.

The “sweet spot”:  When you realize that most human mouths have a similar size and shape, you get smart and create a template based on a random sample of 30 humans.  You now have a general, plastic guard for sports, “one size fits all.”   It’s a model that takes enough human parameters into account so that it fits humans well, is representative of a generic mouth, and thus it works well for many different types of people.

Overfitting:  People quickly learn that they can drop the mouth guards into hot water, and then stick them onto teeth to get an almost perfect fit.  With this in mind, you throw away your generic template, and decide to create all mouth guards in this manner (of course washing them to get rid of the germies!)  Now, your training set are the mouths that you fit the guards to before selling them, and the testing set are still your buyers.  But then, to your surprise, you start to get letters from customers that particular spots in the mouth guard are too small or big, have teeth delineations that are completely different from their own,  or just plain don’t fit the mouth cavity at all.  Some people even comment that their guards have more teeth than they do!  Oh lord, what happened?  This is literally a case of overfitting.  Because you have built your model based on the fine details of your training set (the mouths that the guards were specifically fit to, every last bump, lump, and tooth), the guard is not at all extendable to any mouths other than the one it was built for.

The lesson, at the end of the day, is to put some thought into how you test and train your data, and to put together an evaluation strategy that takes the model and the data it is intended for into account.  If you are writing a paper, it’s probably a good idea to extend your model to as much data as your can get your hands on to demonstrate how awesomely robust it is.

Neuroimaging and Neurochemistry of Autism

This article can be found at http://www.ncbi.nlm.nih.gov/pubmed/22284793

There are multiple causes of autism, and we have to rely on behavioral definitions because we can’t define biomarkers

Possible causes:

• Alteration in common signaling pathways
• Alteration of neurotransmitters, implications during brain development - if we can understand what goes wrong with NT, can develop pharmacological intervention

PET and SPECT

used to study serotonin and dopamine and GABA systems

Dopamine:

Together these studies suggest altered dopaminergic function in frontal cortical regions but not in striatum in children and adults with autism

• Ernst et.al reported a 39% reduction of the anterior medial prefrontal cortex/occipital cortex ratio in the autistic group. suggest that decreased dopaminergic function in prefrontal cortex may contribute to the cognitive impairment seen in autism.
• (Transporter) study reported a whole brain increase in dopamine transporter binding in the autism (child) group
• Nakamura and colleagues17 measured dopamine transporter binding in adults with autism, significantly higher in orbital frontal cortex in the autism group compared with 20 age-matched and IQ-matched control subjects

Serotonin:

• Schain and Freedman, increased blood serotonin in 1/3 autistic patients (1961)
• Chugani et al found two serotonin abnormalities: 1) difference in whole brain serotonin synthesis, greater, suggested that humans undego period of high brain serotonin synthesis during childhood and this process is disrupted in autistic children
• Assymetries of AMT uptake in frontal cortex, thalamus, and cerebellum, suggesting a role of the dentatothalamocortical pathway in autism.
• Decreased serotonin transporter binding has been reported in both children and adults with autism.
• Reduction in binding in anterior and posterior cingulate cortices was correlated with impairment in social cognition, whereas the reduction in serotonin transporter binding in the thalamus was correlated with repetitive or obsessive behavior.
• Measured 5HT2A receptors in 8 men with Asperger syndrome, had significantly reduced serotonin receptor binding in total, anterior, and posterior cingulate cortex, bilateral in frontal and superior temporal lobes and in the left parietal lobe. significant correlations with qualitative abnormalities in social interaction with binding reductions in anterior and posterior cortices, as well as right frontal cortex.
• (5-HT2) receptor binding was significantly lower in autism parents, 5HT2 binding potential was inversely correlated with platelet serotonin levels in the parent group

GABA

• Cytogenetic studies reported the abnormalities in chromosome 15 in autism, specifically 15q11 to 15q13, the region encoding several GABAA receptor subunit genes
• Symptoms of autism can be associated with both Prader-Willi and Angelman syndromes, both of which involve alterations in the chromosome 15q11 to 15q13 region (deletion maternal chromosome –> Angelman, paternal –> Prader William) (GABRB3, GABRA5, and GABRG3

NAA

• Most studies report decreased NAA throughout autistic brain
• A study of Asperger syndrome showed higher NAA in the medial prefrontal lobe of the Asperger group (14 adults) compared with 18 age-matched, gender-matched, and IQ-matched adults. The increase in NAA was significantly correlated with obsessional behavior in the Asperger group
• Changes in serotonin synthesis, NAA decreases, and fMRI activation all point to dysfunction of the corticothalamocortical pathway

Modeling Biomedical Systems (BMI 210)

Comprehensive Study tools for BMI 210:

Methods for modeling biomedical systems and for making those models explicit in the context of building software systems. Emphasis is on intelligent systems for decision support and Semantic Web applications. Topics: knowledge representation, controlled terminologies, ontologies, reusable problem solvers, and knowledge acquisition.

Flashcards - BMI210

K-Nearest Neighbor Clustering (KNN)

K nearest neighbor (KNN) clustering is a supervised machine learning method that predicts a class label based on looking at other labels from the dataset that are most similar.  In a nutshell, the only things that you need for KNN are:

• A dataset with N features for M observations, each observation having a class label and associated set of features
• some equation that determines the similarity between any two observations

1) Decide on a distance (similarity) metric to assess how similar any given observation is to another one

When we talk about a distance metric, this means that larger values = less similar.  When we talk about a similarity metric, this means that larger values = more similar.  In this case we will use a distance metric, namely the Euclidean distance.  If we have two vectors, x1 and x2, we want to subtract them from one another, square them, then take the square root:

x1 and x2 being vectors implies that for each matching feature in x1 and x2 we are subtracting, squaring, and then adding them all up and taking the square root.  If you want to work with matrices, simply take the square root of the dot product

2) Construct a distance matrix, where a coordinate (i,j) corresponds to the similarity/distance between observation i and observation j

To prepare for training, we should calculate all of our distances in advance.  This means creating a matrix of size m x m, and looping through every combination of observations, calculating this Euclidian distance and putting it in the matrix in the correct coordinate, (i,J).  This means that the value at (i,j) will be equivalent to the value at (j,i), and if i = j, since we are calculating the distance of an observation to itself, the matrix should equal 0.

3) Set a value of K

The value of K is the number of similar neighbors that we want to look at to determine our class label.  We basically will look at the class labels of the K nearest neighbors of some novel set of features, our X, and then ascribe the label that occurs most often, the idea being that similar things have similar features.  It makes sense, right?  It’s a good idea to set an odd value for K so that you always have a majority class label.  How do you determine this value?  It can be based on some domain knowledge, or commonly we try a range of values and choose the one that works best.

4) How do we “train” the model?

KNN is different from something like regression in that we don’t have to determine some optimal set of parameters.  We can’t determine some parameters and throw the data away - our model is the data itself!  This is called a non-parametric model.  With this in mind, when we are “training” a KNN model, we are basically interested in getting some metric of accuracy for a particular dataset with labels.  The simplest and most obvious solution is to calculate accuracy as the number that we got right over the total.  So we essentially want to iterate through each observation, find the K nearest neighbors based on Euclidian distance, look at their labels to determine a class for the current observation, save the class to a vector of predicted observations, and then compare the predicted to the actual observations to calculate accuracy.

4) How do we evaluate the model?

In the case of KNN, we can’t really say anything about finding a “significant” result.  Instead, it is customary to assess specificity, sensitivity, and generally, all the ROC curve metrics (area under the curve, etc.).  You would want to compare the performance of your model to the current gold standard.  An accuracy of .80 may seem not so great, but if the current gold standard produces something along the lines of .70, you have made marginal improvement!

K-Nearest Neighbors in High Dimensions

Unfortunately, KNN falls prey to the curse of dimensionality.  It’s ok to have lots of observations, but in the case of many features, KNN can fail in high dimensions because it becomes difficult to gather K observations close to a target point xo.

Linear Regression

What is Linear Regression?
What does a dataset look like?
How do we fit a model?
Batch Gradient Descent
Stochastic Gradient Descent
The Normal Equations
Summary

What is Linear Regression?

Linear regression is modeling some linear relationship between a dependent variable, y, and an explanatory variable, x.  We call it a “regression” because our y variables are continuous.  If we were trying to predict a binary outcome we would call it classification, but more on that later.  When we have just one relationship this is called simple linear regression, and more than one is **multiple linear regression, **each relationship modeled by the equation:

y = mx + b

With more than one explanatory variable, each coefficient is represented with beta (b) , and e is some error, or what cannot be explained by the model.

y = b1x1 + b2x2 +…+ bnxn + e

This equation is commonly called our hypothesis for how the different predictors or features (x) predict the outcome (y), and we can rewrite the equation as “h as a function of x”:

h(x) = b1x1 + b2x2 +…+ bnxn + e

We like to use matrices to make computation more efficient, and so typically we write this as a XTB, where X is a vector of explanatory variables, and B is a vector of coefficients.  The errors are captured by a vector represented with the e term.  Note that this equation is just representing one outcome (y) with one set of features (x’s).

You can imagine plotting one dependent (y) against one explanatory variable (x), and if there is truly a linear relationship, we might see something like this:

Simple linear regression with one independent variable

What does a dataset look like?

The equation above models just one y and a set of x.  An entire dataset consists of many y variables each paired with a set of x’s and an error term, and our goal is to find a set of betas (the coefficients) that best fit all of the data.

How do we fit a model?

We use the least squares approach.  Let’s look at the picture above.  We can draw a line from each blue point to the red line.  This represents the distance (error) for each point, or in other words, how off it is from our model (the red line).  If we calculate all these distances, square each one to do away with possible negative, and then add them up, we get the sum of the squared error, also called the residuals.  This number represents how well our model fits the data.  If every blue point falls on the red line, this number is 0.  Larger numbers mean that our data does not fit the model as well.  This metric is going to allow us to figure out the best fit model for any set of points - we want to find the values of beta (the coefficients) that minimize this least squared error.  This equation that represents the goodness of fit of a model is called a cost function.  If we minimize the cost function, then we find the best model to fit the data.

Batch Gradient Descent

1) Write an equation that represents the sum of the squared errors, the least squares cost function:

In this case, we are summing from 1 to m, where m is the number of cases we have in our dataset, each with one outcome variable (y) and a set of (x).  This equation represents exactly what we discussed above - h(x) is our model’s prediction of the outcome based on the features, y(i) is the real outcome, and so h(x) is the difference between the actual and observed outcome, our error, which we square, and then sum up for all of our m data points.  This equation gives rise to the ordinary least squares regression model.

2) Minimize the least squares cost function:

**To find the set of betas that best fit out data, we should aim to minimize the cost function.  We can do this with **batch gradient descent, where we will randomly initialize our beta values, and then “take a step” in the steepest direction to find a minimum.  This means that we are interested in the rate of change of the function, so we are going to want to take the derivative.  We will basically take steps and update our beta values each time until we decide to stop taking steps.  If we took the derivative for just one training case, we would get the following update rule:

where a is alpha, the learning rate, **or how big a step we want to take.  And this has a particular name that you will never remember, but I’ll share anyway: the Least Mean Squares or Widroff-Hoff **update rule.  Remember that the subtraction in the parentheses represents how far off our prediction is from the actual value.  If this value turns out to be small, that means that our parameters don’t change so much.  If it’s large, they do!  To extend this equation to batch gradient descent, we would do:

**Repeat until convergence, for every training example, j

Convergence might mean that the parameters stop changing, or a certain number of iterations have occurred, or some other logical criteria.  And wait a minute, isn’t that a quadratic function? Yes! This means that we always converge to a global minima.  The final model is the coefficients that we converge to, woohoo we are done!

Stochastic Gradient Descent

Guess what? We don’t necessarily have to look at every training example before “taking a step.”  What if we have a HUGE dataset, and looking at every training example is infeasible?  We can use stochastic gradient descent!  It’s almost exactly the same, except we update J(x) after looking at each of the m training examples.  The new update equation becomes:

for i=1:m {

xj = xj + a (h(x)i) - y(x)i)^2 * xj

}

This will let us hop around the hypothesis space much faster, although we may never completely converge (although we are usually very close).

The Normal Equations

Linear algebra gives me shivers, but it’s worth mentioning that there is a much more efficient way to solve this problem: a closed form.  We can represent our data and unsolved regression coefficients in matrices, and then just solve a matrix form equation to find the values of our betas that minimize the least squared error.  While I’m sure you would enjoy me coughing through the linear algebra derivation, I’m just going to give it to you, because like I said… shivers!  Welcome to the 21st century when you can plug this equation into a computer (Matlab, anyone?) and not need to write it out on paper.

X = (XTX)^(-1)XTy

where X is our matrix of features (the transpose is like squaring it), y is the vector of observed outcomes (remember this is supervised learning so we have labels!)  If you want the lovely derivation, I suggest you take CS229 Machine Learning.  :)  You can plug that into Matlab and get the answer with one line, no looping needed!  That is pretty awesome.

Summary

We’ve learned how to create a model using a dataset with outcomes (y), each associated with features (x) for which the relationship is linear.  All that we did is find the coefficients that minimize the sum of the squares,or the error.  However, before trying to fit any models, I can’t stress enough the value of looking at your data.  You can use almost any software to plot y against different x, and if there is a linear relationship, you will see it!  You can also get a sense of if there are outliers in your data, and if another model might be a better fit.

FDR Correction

The False Discovery Rate (FDR) is a method used to correct for multiple comparisons in a statistical test. It is abstractly a method that gives us the idea of the false positive rate not for one single hypothesis, but for the entire set. For example, if we have brain imaging data and are doing a voxel-wise two sample T-test to look for significant differences between two groups, we are essentially testing a single hypothesis at every single voxel. Let’s say that we have 86,000 voxels. Each of these voxels can be thought of as a feature, with the identifying information being the x,y,z coordinate.

Let’s say that we have two groups, Elevator Repairmen and Opera Singers, and we have structural imaging data and want to know if there are any brain regions with gray matter volumes that are significantly different. The outcome that we are generating is, for each voxel, “yes, the group means are different” or “no, the group means are not different.” If we do our 2 sample T-test to compare the means of the two groups at each voxel, then we will get 86,000 p-values. How do we know which ones are significant, meaning that the difference is likely not due to chance?

Well of course, if it’s less than .05, that means it is significant, right? That means that there is less than a 5% chance that, for each test, we have a 5% chance of having a false positive. Wait a minute… compounded by 86,000 voxels? This means that 5% of our 86,000 voxels are expected to be false positive, which is simply not acceptable. What we need is a standard metric that represents our chance of having a false positive across the entire hypothesis space. Introducing, the FDR, false discovery rate!

The False Discovery Rate (FDR) looks at the distribution of p-values to provide information about the type I error rate across the entire brain, represented by a q-value. What is the difference between a q-value and a p-value? From the literature:

Given a rule for calling features significant:

“…the false positive rate (p-value) is the rate that truly null features are called significant
The FDR (q-value) is the rate that significant features are truly null.”

“A false positive rate of 5% means that, on average, 5% of the truly null features in the study will be called significant. An FDR of 5% means that among the features called significant, 5% of them will be truly null.”

“a q-value threshold is the proportion of features that turn out to be false leads.”

It is intended to both maximize finding significant results while minimizing false positives. You can use a Matlab function, mafdr, with a vector of p-values to get a q-value for each one. How are these two related?

• as p-values increase, q-values also increase (or stay the same)
• we choose a q-value threshold (between 0 and 1) that represents
• “the fraction of p-values with q-values equal to or less than this q-value which, when called ‘significant,’ are actually bogus.” - Dan Golden

This gives us confidence that if we have actual signal, we will have low q-values. If we set our q-value threshold at .05, then we label features (voxels) at or less than .05 as significant, and we can be confident that 95% of our features are probably true positives, and 5% false positives. And you can share your q-value threshold with other researchers to let them decide if they like the result or not.

In a nutshell

FDR is an estimate of the percentage of false positives among the categories considered enriched at a certain p-value cutoff. This is calculated by performing the same analysis on your test data and permuted data. The number of positive results in the permuted data at a given threshold is considered the number of false positives you expect to get if using that threshold for your test data, so the rate is just the number of positives in the permuted data divided by the number of positives in the test data at a given cutoff.

# positive permutations              @ a particular cutoff
# positive tests

Why you should not publish without FDR:

• It’s hard to prove/disprove false results - studies without significant findings don’t get published.
• Lots of time and money could be wasted trying to prove a result that never existed in the first place.

Why not Bonferroni?
In fMRI, since we like to smooth things, there are very likely spatial correlations, and Bonferroni (dividing the p-value by the number of hypotheses, N) does not take this into account.

Functions and Resources

• Matlab FDR Function
• Significant Signal in fMRI of an Atlantic Salmon (why you need to use FDR)!
• Statistical Significance for Genome Wide Studies
• The Principaled Control of False Positives in Neuroimaging

Brain Message 1.0 to Write Secret Messages into fMRI

Have you ever seen interesting shapes emerge as components when running independent component analysis (ICA) on resting BOLD functional MRI (fMRI) data? What comes to mind is the one time I swear that I saw the Koolaid Pitcher mascot, and V1 (visual cortex) commonly looks like a heart (some people do in fact have love on the brain!)

Inspired by these shapes, and wanting to add a bit of fun to bmi260, a course I am TAing this quarter, I decided it would be fun to do a decomposition of functional data and find surprise messages.

What does Brain Message do?

I created a quick Matlab script to do exactly that. It takes as input a specified message, and an output file name, and outputs a nifti file for use with independent component analysis:

dummy = BrainMessage(‘message’,’output.nii’);

You will want to create the image using the command above, and then run ICA. I normally use FSL’s melodic, however another good option is the GIFT toolbox, for those users who prefer Matlab and SPM. The script uses SPM to read and write images, and you can of course change these function calls to your preference. When running ICA, you can estimate the number of components or use your method of choice, however I will tell you that 46 should work best.

Here is an example letter:

How does it work?

I basically start with a set of real component timecourses and spatial map distributions, and modify the spatial maps to take the shape of letter templates. The algorithm solves for the matrix W in the equation S = W X, where S is the observed signal, W is some matrix of weights, and X is the unmixed signal. Applied to fMRI, our matrix of weights consists of columns of timecourses, and the unmixed signal has rows of component spatial maps. I therefore went about this backwards, and multiplied rows of timecourses with edited spatial maps to come up with the observed data, S. In other words, for each letter, we multiply a column of Nx1 timepoints by a squished spatial map (a row of 1xV voxels) to result in a matrix of size NxV. I then decided to add in some real functional network spatial maps to make the data more realistic.

Where do the templates come from?

These three sets of templates come zipped up with the script, and there are 46 of them, meaning that you are limited to creating messages 46 characters long. Why did I choose to do this? I wanted this data to be as “real” as possible as opposed to the other option of generating random timecourses and distributions. You could easily edit the script to make everything faux and remove this limit. Secondly, I wanted uncovering the letters to not be consistently easy. By using real data I would be sampling from components with varying strength, and so a resulting spatial map can come out weaker by chance, making seeing it more challenging.

What can I change?

You can easily modify the script to generate fake timecourses, and not limit to messages of 46 characters. You can also create new templates (smiley faces, custom logos), or improve the code however you see fit. Have fun!

Download Scripts

MATLAB libc.so.6 not found error Fix

For as long as I’ve had linux, my MATLAB spits out the following “not found” error on startup:

.../MATLAB/bin/util/oscheck.sh: 605: /lib/libc.so.6: not found
</pre>


However it is clear that I have the library:


locate libc.so.6
/lib/i386-linux-gnu/libc.so.6
</pre>


The answer is to create a symbolic link from this library to your machine’s standard lib folder, as follows:


ln -s /lib/i386-linux-gnu/libc.so.6 /lib/libc.so.6
</pre>


…and you will never see the not found error again!

The Lorax

when drips a little puddle
escaped from cocoa spoon
he sees inside the muddle
the lorax in his room
behind the wall a pip
and dance a veiny maze
this reflection that he sips
this awkward, curly gaze
a laugh so shrill,
a voice so near
a tummy far away
a love to nill
a sense of fear
a heart that does dismay
dry up the puddle might
and he will wipe away
his hopes and dainty fright
for maybe one more day
for deep down he knows
that lorax come undone
for deep conviction he goes
the safest route as one

I Do Not Want to Be A Drowning Duck: the treadmill of graduate school

I don’t have enough time to play. Even in absence of most social activity outside of research and weekends devoted to work, the play is just not happening! Why is this problematic? It is problematic because I strongly believe that a researcher can be his or her greatest when only subjected to self-derived constraints. The most productive and interesting times of my young academic life have been when I find a cool method, and am independently driven to understand and extend it. That might include reading about statistical methods or mathematical principles that I do not understand, or diving into a tutorial to learn nuts and bolts. The idea is that the responsibility to explore is my own, and given that the catalyst is personal interest (and sometimes stubbornness), I would argue that this is the secret formula for creativity and productivity. I would hope that I was chosen to be a graduate student based on this intrinsic hunger for understanding, learning, and building things! This quality that emerges from the woodwork does not require an external hand of control. In fact, when you add this external control to the equation, the resulting sculpture is ruined. What might have emerged from the block is of an entirely different vision and hand. Thus, I want to argue that to best develop as a researcher, I must maintain control of my tools. I must have time to play.

Let’s start by breaking apart the composition of graduate school, which is me-as-a-researcher in the short term. The first two years are a whirlwind of trying to fulfill class and research rotation requirements, with the general idea that you should both be improving your computational prowess and finding your niche lab. There are a few courses that feel lovely in how I can see the relevancy, and a lot more courses that give me what unfortunately feels like busy work. Given my focused personality and desire for efficiency, when I feel that I am not learning or using my academic credits as wisely as I might, this is troubling. I will admit that I made the mistake of taking a handful of domain courses to supplement my research when I should have immediately jumped into strictly methods and computational ones. However, I would also argue that I was pushed into the domain knowledge courses due to the pressure to be able to propose marriage to a lab within a handful of rotations. How am I supposed to know if the domain is right for me if I have yet to explore it more deeply? All in all, the takeaway point here is that both of these components take up every ounce of my little graduate student soul, and leave no time for anything else.

Let’s now talk about me-as-a-researcher in the long term. The ultimate, and ideal goal is to identify a core problem that I am both interested in, AND good at. If I am good at something and not interested, that’s like putting a cat in a room with a small dog. The cat could probably tear him apart, but he’s thinking about a delicious mouse. If I am interested in something but not good at it, well then I could either become good at it or just be mediocre and happy, but then I wouldn’t be able to really have an impact and it’s probably not a good use of time assuming that the ideal algorithm is to match people with what they are best at. Ideally, I would want to be able to have at least a sense of this particular problem that I want to pursue by the end of two years, giving me approximately 3 to 4 years to pursue that and nothing else! The “end” of the journey is a beautiful and passionate dissertation to earn a PhD, and then stepping into a new set of academic shoes. For now, we will stay within this journey of obtaining the PhD. I would now like to explain why I need time to play in these first two years, a dynamic that is not supported by the current structure.

In middle-school, high-school, and college, the world was very narrow. There was a small set of well defined problems, handed to me by the teacher, and I could prove mastery by solving them and getting the best grade in the class. Never did I have to think about problems in the “real world” and I certainly didn’t have to define my own problems and independent plans of action for pursuing them. This flipped dynamic is of course definitive of graduate school! For the first time I am seeing so many interesting problems, and so many various sub-problems (even under the same domain umbrella)… which one to choose? I know that I am smart and capable, and making this choice is a matter of:

1. identifying said core problem
2. hammering down resources for learning, and allocating time to make sure I have the breadth and depth to have domain mastery
3. pursuing a specific question with this mastery

and at some point hovering around steps 2 and 3 I might transition into a “real” researcher. This train of thought is why I do not believe that it make sense to publish in the first, second, or X year of graduate school. How can one so quickly identify, understand, and conduct meaningful research about any particular domain? I know that the rule of the road is publish or perish, but I most certainly don’t want to publish for the sake of publishing. Just having a result does not mean it is worthy of telling the rest of the world. I am sure that many young graduate students pursue guided work that is meaningful and should be published, however largely I think that meaningful contributions are more likely to take half a decade of work… or a large nugget of a lifetime! A large percentage of papers that do get published by dewy, green graduate students probably are not that great. However, I digress! This process of identifying and being ready to pursue a problem should be the goal after two years.

The pressure of the short term goals (paragraph 2) is what endangers this process. It is very likely that one can be so overwhelmed with other things that they are unable to choose at all, or choose the wrong domain or question due to not having enough time or mental energy to explore. Let’s go back to talking about my little busy-graduate-student brain. It is latched on again to the high-school and college mindset of cranking out problem sets, preparing for exams, and trying to meet expectations of advisors and professors because I am being stamped with grades and forms with long lists of requirements. It should not matter, and even when I intellectually acknowledge this dynamic, I cannot get around the fact that learning is a different experience when I feel it is forced as opposed to being my own exploration and choice. When I learn something fantastic, and a little light goes off in my head of something I am eager to play around with, I always find myself asking “so when can I get to try that out?” The answer is usually some convoluted “at some time in the future.” I then add it to the place where ideas go to die, a list of things in a Google Doc that are delayed indefinitely because I have to prioritize everything else. The irony is that the exploration of these little ideas, being allowed to play, would better lead me to identify my focus, and lead to more productive work.

If we were real scientists or researchers, we would be driven by those little impulses to play with ideas. I would feel a spark, and perhaps work for a week on Idea 1, go for a month on Idea 2, identify a gap in my knowledge and spend time just reading, and focus the courses that I take based on these gaps. I would hungrily run around to every lecture that I find interesting, and be given the freedom and trust of using my time in a way that will lead to the two year goal of identifying a domain and problem. There would not be expectation of sitting in any particular chair for X hours a day to fulfill some confusing requirement, or taking a course of flavor Y because someone else is convinced I will be incomplete without it. This level of control, namely how every quarter I have to take an overloaded number of courses (no matter what!) and do X,Y,Z in a rotation (no matter what!) is suffocating and stifling. I largely do not have a choice. If I do not sign my name on the line and get everything done, I won’t fulfill requirements by the end of two years and can chance losing funding, which is the equivalent of death for the graduate student. The problem is that during these two years we aren’t allowed to be real scientists, yet after two years it is what will be expected of us. We aren’t allowed to follow impulse and passion and idea because there just isn’t time, and by the time we are given time (after courses are over) we have already proposed marriage to a domain / lab that may not have been the choice had we time to explore. The carving might turn into a dancing penguin when it would have been a contemplative giraffe.

So, this is the fundamental problem in my head. I feel an urgency and a drive to find “that problem” that I think I could both be good at AND make a difference. But that is in conflict with what I think I should be doing now, which is learning how to ask better questions and developing a computational background that is going to give me the ability to answer those questions. To have a program structured that forces the student to do both at the same time does in fact the exact opposite, because there is no time to play. Neither domain or intellectual depth is reached. And this problem is not limited to any particular institution. I love my school. I know that I am in the right program, and am blessed to have more freedom than the average graduate student. However, I yearn for less control and more freedom to run around taking in as much knowledge goodness I can be present for, pursuing projects with fellow graduate students driven by intellectual curiosity, and growing as a real researcher as opposed to an individual trying to fulfill what others expect of her. This is why I want to play, and even if I cannot, I will stand on this little soap-box and declare it to the world. I will continue to plow up this hill with hopes that after two years, the environment that I might find at the top is the same place I would have decided to want for myself.

GIT Basic Commands to Update Repository

This summer I started to use github as a repository for my code, and I wanted to document instructions for updating a repository. This is assuming you already have created the repository, and have the appropriate .git folder on your machine, the local repository!

Get the status of your local repository

# Shows files that you have in folder, which ones are added (A) or modified (M)
git status -s

Set up your credentials

# credentials
git config --global user.name 'My Name'
git config --global user.email 'myemail.address'

Adding new files to your local repository:

git add file1 file2

Commit files to the local repository

# commits the files to your local repository -
# this will bring up a text document and you can
# uncomment the files that you want to commit, save, and exit.
git commit -a

Send to github repository

git push origin master

MRlog to create text log of nifti brain images

Gone are the days of having messy, disorganized directories of neuroimaging files! Or, in my case, needing to process 800 datasets, for which each subject has three runs, and not knowing which one has the correct number of timepoints!

This python script takes in a top directory (to search all directories underneath) for nifti (.nii or .nii.gz) files, and then uses fsl or the MRtools module to read header data and output a list of images with paths and important information.

• MRlog: Details, usage, and the scripts
• Github: Straight to the script!

Kaustubh Supekar

…or as I thought of today, “Supe-Kau!” ;O)

](http://www.vsoch.com/blog/wp-content/uploads/2011/07/supe-kau.png)Supe… ah, say no more! I know exactly of the man you seek.